Pranostiky sú ľudové múdrosti predpovedajúce počasie, ktoré je známe predovšetkým svojou nepredvídateľnosťou. Podľa všetkého pranostiky zľudoveli najmä preto, lebo dobre zneli, a nie preto, že by sa zakladali na štatisticky overených skutočnostiach.
Cieľom tohto textu nie je vedecky vyvrátiť či potvrdiť pranostiky – predsa len ich iba málokto berie úplne vážne. Zámerom je skôr ukázať, ako vedci pristupujú k skúmaniu sveta okolo nás.
Na základe dlhodobých pozorovaní mnohí očakávame, že keď sa skončí leto a ochladí sa, po nejakom čase sa ešte pred definitívnym príchodom jesene zasa na pár dní oteplí. Hovoríme tomu babie leto. Počasie teda nie je úplne náhodné a jeho sledovanie ľuďmi sa pretavilo do pranostík, z ktorých mnohé sú veľmi známe a populárne. Sú pranostiky jednoducho destilovaná múdrosť mnohých generácií, odpozorované nenápadné štruktúry, ktoré si človek za bežných okolností len tak nevšimne?
Rozhodol som sa túto možnosť otestovať. Ako fyzik momentálne pracujem na numerických simuláciách kvantových modelov. Znie to sofistikovane, značná časť práce však spočíva v spracovávaní veľkého množstva údajov, v hľadaní ihly v digitálnej kôpke sena. Prirodzene som tak pri pranostikách siahol po rovnakom nástroji – napísal som krátky počítačový program, ktorý analyzoval dostupné historické údaje z niekoľkých meteorologických staníc a hľadal v nich oporu pre niektoré známe pranostiky.
Bude zajtra pršať?
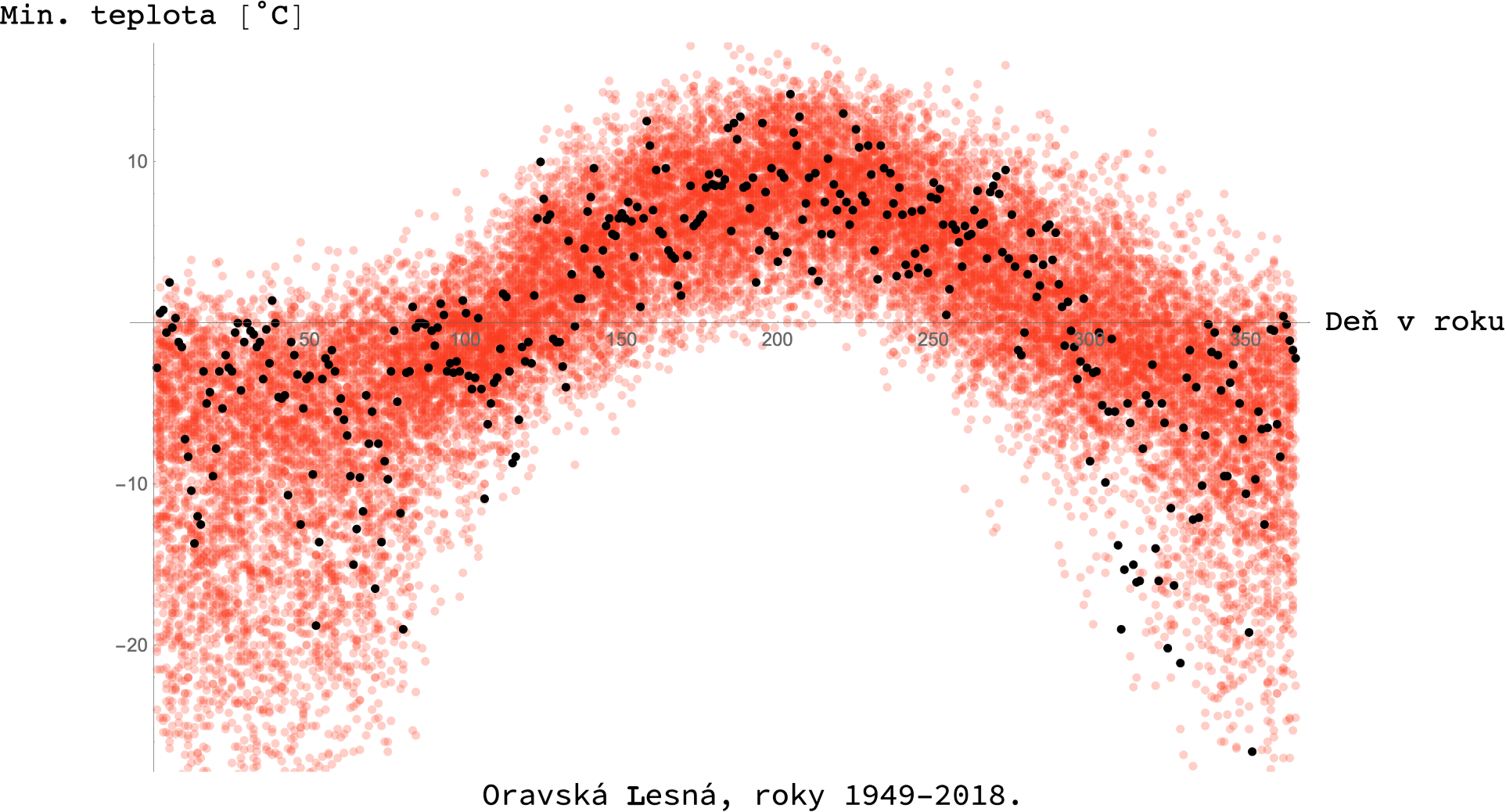
Keď je počasie niečím typické, tak svojou nepredvídateľnosťou. Zbalíte si veci na piknik, pod jednu pazuchu si dáte deku, pod druhú slnečník, vykročíte z domu a na hlavu vám začnú padať veľké kvapky. Dupnete si nohou: Zasa mali zlú predpoveď! Nehnevajte sa preto na meteorológov, robia, čo môžu.
Fyzikálne modely poznajú rôzne formy zložitosti. Niektoré systémy sú malé, ale opísané zložitými rovnicami, ktoré obsahujú veľa detailov. Iné systémy majú zdanlivo jednoduché správanie, ale mnoho previazaných zložiek – práve ich početnosť výpočty nesmierne komplikuje. Kým niektoré systémy sú veľmi robustné, ďalšie hraničia s chaotickým správaním – drobná nepresnosť v úvode sa premení na obrovské chyby vo výsledku. Meteorológovia bojujú so všetkými týmito problémami. Počasie je chaotické, teda je citlivé na presnosť vstupných dát. Správanie zložiek atmosféry opisujú zložité rovnice a systém sa skladá z mnohých menších dielov, ktoré sa navzájom ovplyvňujú. Napríklad vieme povedať, že 2. júna 2095 bude z Namíbie vidno úplné zatmenie Slnka, no netušíme, či bude 2. júna 2020 v Terchovej pršať alebo nie.
Správne položená otázka
Na druhej strane, nie všetko je nepredvídateľné. Je pomerne bezpečné tvrdiť, že v zime budú v priemere nižšie teploty ako v lete. Alebo sme zvyknutí, že po najväčších horúčavách v lete prichádza búrkové obdobie. Tento jav má určite svoje meteorologické opodstatnenie. To však nemusíme poznať, aby sme si pravidelnosť tohto javu všimli. Zaregistrovali podobne naši predkovia aj oveľa nenápadnejšie detaily vo vzorcoch počasia? Alebo sú pranostiky len niečo, čo sa hovorí?
Bude zajtra pekne? To je otázka, na ktorú veda nevie odpovedať, pretože nie je jasne definovaná. Počasie je subjektívna záležitosť, niekto má rád slnečno a niekto sychravo. Vedci sa snažia svoje otázky definovať čo najexaktnejšie, aby im dal výsledok experimentu jasnú odpoveď. Bude zajtra v Oravskej Lesnej maximálna denná teplota nad 35 °C a nulový úhrn zrážok? To už je otázka, na ktorú môžeme dať jasnú odpoveď. (V tomto prípade je odpoveď takmer určite: Nie, nebude.)
Musíme teda sformulovať pranostiky tak, aby sa dali jasne overiť. To však môže byť problém, pretože pranostiky sú často nejednoznačné. Zoberme si napríklad: Medardova kvapka, štyridsať dní kvapká. Znamená to, že prší nepretržite 40 dní a ani na minútu neprestane? Alebo 40 dní po sebe prší každý deň aspoň chvíľu? Alebo je to 40 dní, keď prší nadpriemerne veľa? Dážď trvajúci 960 hodín bez prerušenia si asi nevieme predstaviť, preto prvú možnosť ani netreba testovať.
Ako na to
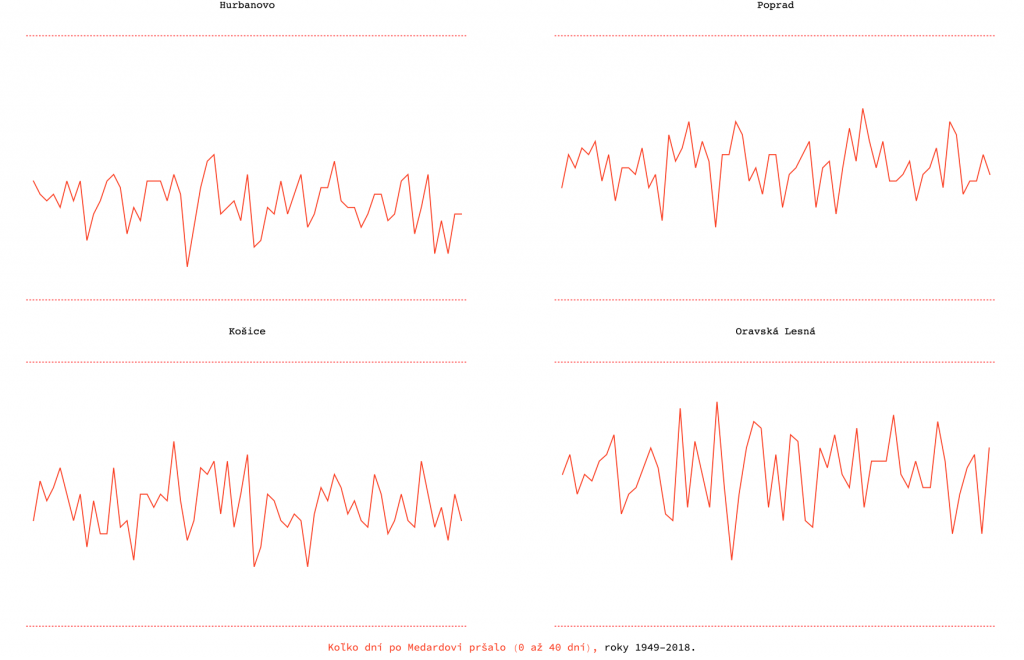
Koľko dní po Medardovi teda naozaj prší? Odpoveď som hľadal pomocou historických údajov zo štyroch meteorologických staníc (Hurbanovo, Poprad, Košice a Oravská Lesná) za 70 rokov – spolu som mal k dispozícii asi 300 000 číselných údajov. S vyhodnotením mi pomohol program, ktorý jednoducho prešiel všetky dostupné záznamy a vytvoril grafy.
A výsledok? Po Medardovi prší relatívne dosť, v priemere asi polovicu dní. Všimnúť si možno aj jeden rekord – v Oravskej Lesnej pršalo počas tohto obdobia až 34 dní, a tak predpoveď takmer vyšla!
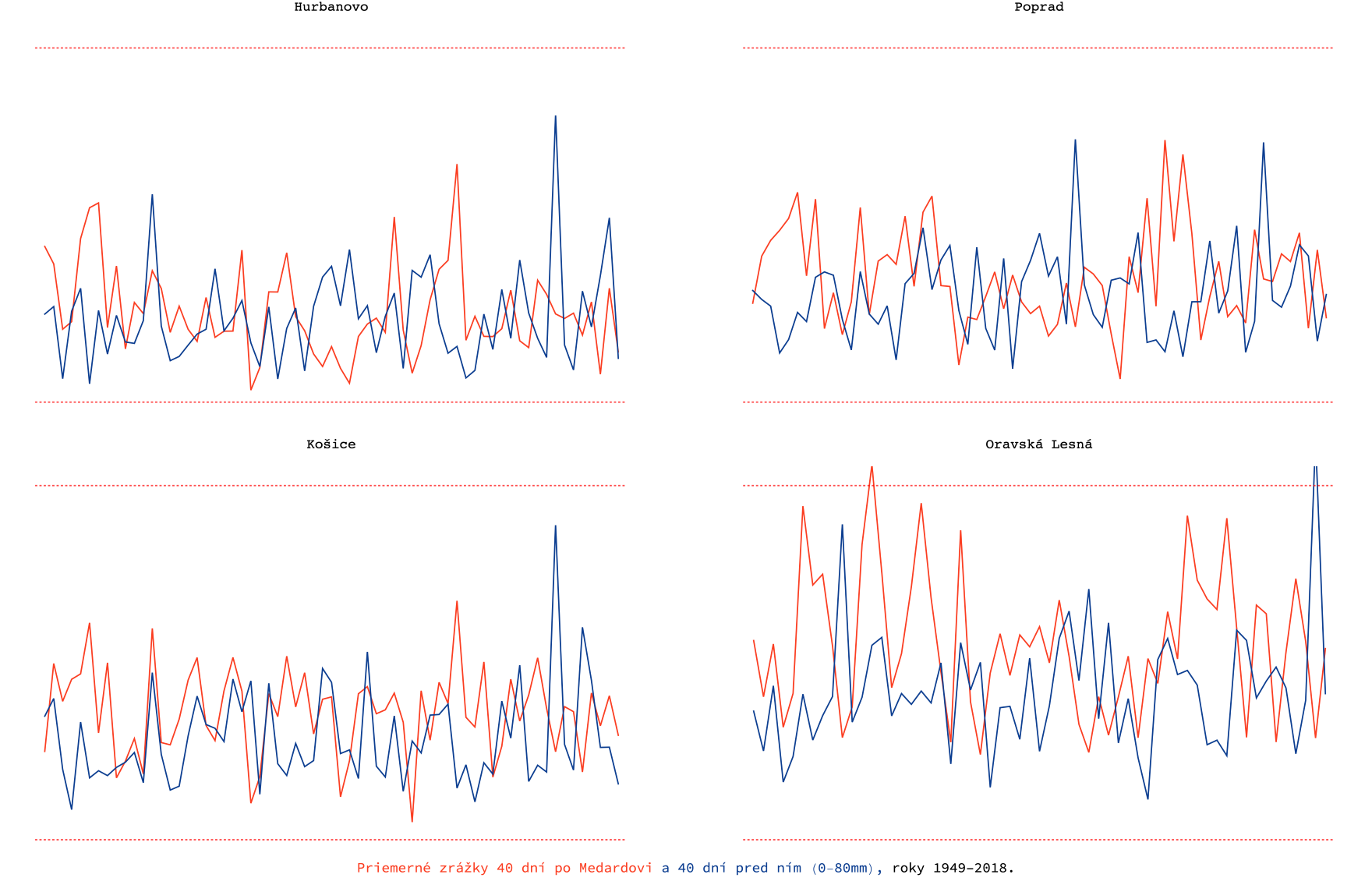
Prší 40 dní po Medardovi viac, ako pršalo 40 dní pred ním? Áno! Samozrejme, ako kde. Kým v Hurbanove je to takmer rovnako, v Oravskej Lesnej je trend výraznejší. Väčšinu rokov, až 80 % z nich, je úhrn zrážok väčší po Medardovi ako pred ním. Vo všetkých štyroch staniciach však platí, že po ňom prší väčšmi ako pred ním, a tak je na mieste otázka: Prečo? Toto je niečo, čo nám naše údaje nedokážu ukázať. Odhalili nám súvis, no nie jeho pôvod. Odpoveď by sme museli hľadať u meteorológov. Tí by nám povedali, že za to môže atmosférická cirkulácia, ktorá nadobudne západný charakter – z Atlantiku k nám dorazí vlhký oceánsky vzduch. Takéto relatívne predvídateľné a pravidelné výchylky z trendu počasia sa volajú singularita.
Celá veda
Kľúčovým nástrojom na hodnotenie pranostík je štatistika. Vystačíme si s dvoma pojmami – prvý je priemer (respektíve stredná hodnota), druhý korelácia. Možné synonymum korelácie je aj prepojenie. Veľa pranostík má totiž formuláciu: Keď sa jeden deň stane toto, druhý deň sa stane tamto. Korelácia nám hovorí o tom, ako sú dva súbory čísel prepojené. Napríklad, dva súbory čísel (1, 2, 3) a (2, 4, 6) sú pomerne očividne prepojené. Konvencia je taká, že ich koreláciu označíme ako 1, pričom škála ide od -1 po 1.
Korelácia nám ďalej hovorí, či čísla stúpajú a klesajú oproti priemeru naraz (korelácia je 1), presne naopak (korelácia je -1) alebo nezávisle od seba (korelácia je 0). Príklady zápornej korelácie sú (1, 2, 3) a (3, 2, 1) – keď je prvé číslo veľké, druhé je malé. Nulovú koreláciu predstavujú napríklad (1,2,3) a (1,-2,1) – jedna postupnosť rastie, druhá klesá a rastie, sú teda od seba nezávislé.
Korelácia bez kauzality
Známa mantra kritického myslenia znie: Korelácia neznamená kauzalitu. V lete stúpa množstvo skonzumovaných zmrzlín, aj množstvo ľudí utopených v jazerách – medzi týmito javmi je teda korelácia, pravdepodobne však nie kauzalita. Zmrzliny nespôsobujú utopenia a ani naopak, utopenia nespôsobujú, že ľudia dostanú chuť na niečo sladké. Obe majú rovnaký pôvod: je teplo, ľudia tak majú chuť na niečo studené a zároveň trávia viac času kúpaním – a tak sa aj viac z nich utopí. Zamieňať si koreláciu s kauzalitou je nebezpečná skratka, ktorej sa musíme vyvarovať. Oddeliť koreláciu od kauzality býva všeobecne veľká výzva, najmä v medicíne či v spoločenských vedách.
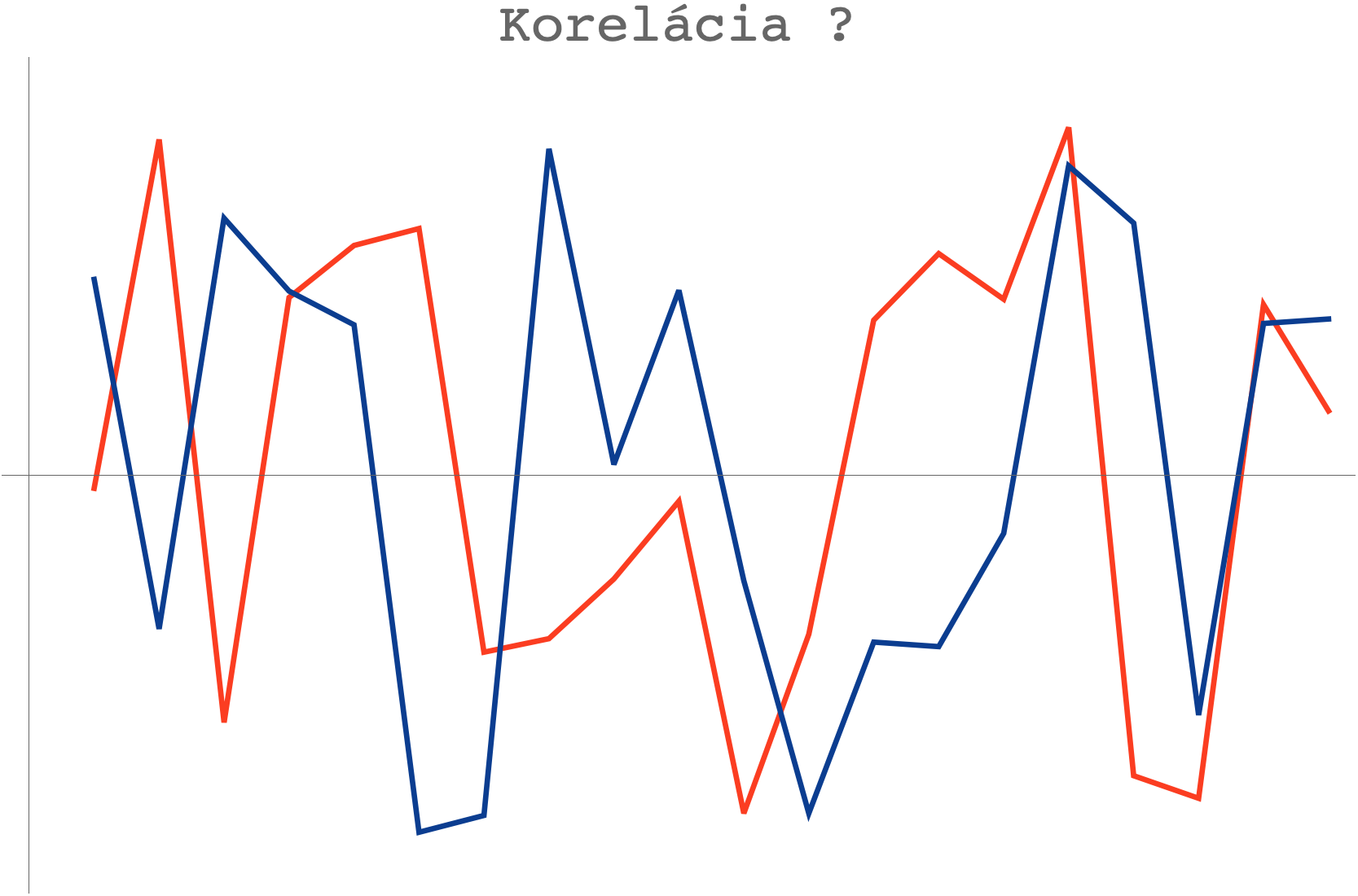
Zľava doprava rastie korelácia, od -1 po 1. Dokonale zladené alebo dokonale rozladené grafy sa dajú predstaviť ľahko, užitočné sú však druhý a štvrtý graf. Ukazujú nám, čo si možno predstaviť pod miernou koreláciou.
Dobrou správou teda je, že nás zaujíma korelácia, nie kauzalita. Katarína na blate nemusí spôsobiť Vianoce na ľade, oba tieto javy môžu mať nezávislú príčinu. Atmosféra nie je úplne chaotická, javí rôzne dlhodobé trendy a pokojne sa môže diať, že tá istá anomália, čo zablatí Katarínu, zároveň zamrazí Vianoce.
Zaujímavou vlastnosťou korelácie je, že ju nezaujíma veľkosť čísel, ktoré porovnávame, ale iba to, či sa menia voči svojmu priemeru synchronizovane alebo nie. Dovolil som si teda mnohé grafy preškálovať tak, aby boli v rozsahu od minimálnej po maximálnu hodnotu v danom období. Grafy rôznych veličín, napríklad teplôt a úhrnu zrážok, nám tak budú spolu pekne sedieť.
Text a grafy Samuel Kováčik
Dublin Institute for Advanced Studies
