Vladimír Alexandrovič Džanibekov je bývalý sovietsky kozmonaut. Na rakete letel do vesmíru päťkrát. V súčasnosti sa však jeho meno spája s inou raketou – tenisovou.

Začnime tento text experimentom. Zoberte si knihu s pevnou väzbou alebo, ak si trúfate, svoj mobilný telefón. Cez knihu idú tri hlavné rotačné osi: zľava doprava x, zdola nahor y a zozadu dopredu z. Skúste teraz knihu vyhodiť do vzduchu a pritom otočiť o 360° okolo osi z, ktorá ide cez čelnú a zadnú stranu knihy. Stále vidíte prednú stranu knihy a tá sa točí, ako keby bola položená na platni. Bolo to ľahké, však? Druhý ľahký trik je knihu vyhodiť a pritom otočiť okolo osi y, ktorá ide zhora nadol.
Experiment na ISS
Teraz príde tá ťažká časť – skúste knihu hodiť a otočiť okolo tretej osi, x, teda tak, že vrch knihy smeruje k vám a spodok od vás. Podarilo sa? Je možné, že nie, do pohybu sa vám vtesnala ešte nejaká ďalšia rotácia. Chceli ste knihu otočiť o 360° okolo jednej osi, no ona sa k tomu otočila napríklad o 180° okolo ďalšej. Takýto efekt si všimol V. A. Džanibekov pri manipulácii istou súčiastkou v beztiažovom stave. Súčiastka sa točila okolo jednej osi a raz za čas k tomu pridala salto ešte v ďalšom smere. Prečo sa to dialo? A nemôže sa to stať aj iným rotujúcim objektom? Napríklad celej planéte? Tento efekt poznajú aj hráči tenisu, raketu ľahko otáčajú spolu s rukoväťou a raketa sa točí stabilne, aj keď ju od zlosti hodia ako bumerang. Ťažké je však hodiť raketu tak, aby sa hýbala výpletom k nám, rukoväťou od nás a k tejto rotácii sa nepridala žiadna iná. Efekt teda voláme aj efekt tenisovej rakety, je to rovnako demonštratívne ako Džanibekov príklad so súčiastkou na Medzinárodnej vesmírnej stanici ISS.
Stabilná a nestabilná rotácia
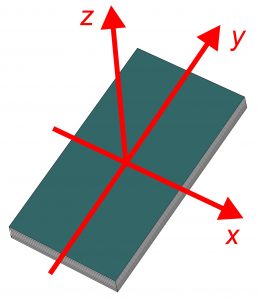
Na pochopenie efektu si treba ujasniť ešte dva pojmy: hlavné osi rotácie a stabilita. Akokoľvek nepravidelný tuhý objekt si vo svojom okolí vyberiete – či už ide o knihu, raketu či zemiak, môžete ho roztočiť ľubovoľným spôsobom, no rotácia okolo troch na seba kolmých osí je v niečom najprirodzenejšia. Toto je dôsledok jednoduchej algebry. Stabilný pohyb je taký, že ak pri jeho nastavovaní spravíte malú chybu, tak sa s pohybom nič výrazné nestane a bude prebiehať v podstate rovnako. Keď spustíte loptu z kopca z jedného miesta alebo o kúsok vedľa, bude sa valiť takmer identicky. Naopak, nestabilný pohyb je citlivý na malé nepresnosti, ktoré postupom času narastú do veľkých odchýlok. Ak sa usilujete vybalansovať vajíčko na futbalovej lopte, tak čo i len milimetrová nepresnosť spôsobí, že ho rozbijete. Kniha, raketa či Džanibekova súčiastka majú všetky tri hlavné osi rotácie – to sú tie tri osi, okolo ktorých sme objekty chceli roztočiť. Pri dvoch z nich bol pohyb stabilný, objekt sa točil len tak, ako sme chceli. Pri tej tretej osi to bolo zložitejšie. Prečo? Keď sa opýtate fyzikov, bežne napíšu pohybové rovnice, prstom ukážu na znamienko jednej z nich a povedia, že je to kvôli nemu – rotácia okolo jednej z osí naozaj pripomína snahu vybalansovať vajíčko na futbalovej lopte.

Coriolisova sila
Existuje aj intuitívnejšie vysvetlenie. Pri rotácii pôsobia na teleso odstredivé sily (v sústave, ktorá rotuje spolu s telesom) a tie môžu spôsobiť, že ak sa teleso trochu vychýli, tak bude výchylka narastať – odstredivá sila ho odtláča od pôvodnej polohy. Prečo sú však niektoré rotácie stabilné a niektoré nestabilné? Lebo okrem odstredivej sily na teleso pôsobí aj Coriolisova sila a tá dokáže efekt odstredivej zvrátiť. Kedy sa jej to podarí a kedy nie, záleží od detailov rotujúceho objektu, najmä od rozloženia hmotnosti v ňom. Vo výsledku sú rotácie okolo dvoch osí stabilné a okolo tretej nestabilné. Tento efekt funguje pre ľubovoľné teleso, ktorého momenty zotrvačnosti okolo hlavných osí sú rôzne. V prípade knihy či mobilu teda funguje len vďaka tomu, že majú inú šírku, hĺbku a výšku. So symetrickým telesom, homogénnou guľou či kockou by efekt nefungoval. Naša Zem síce nie je dokonalá guľa, no má ku guli blízko, ide o veľmi symetrické teleso a tak sa takéhoto prekvapivého salta nemusíme obávať.
Samuel Kováčik
Fakulta matematiky, fyziky a informatiky
Univerzita Komenského v Bratislave
Viac podobných článkov nájdete na stránke vedator.space.






