Dĺžka, šírka a výška – to sú tri štandardné údaje pri meraní rozmerov, vzdialeností a pozícií v priestore. Za štvrtý rozmer mnohí považujú čas. V matematických aplikáciách, ba dokonca aj v každodennom živote však často používame aj štvrtý priestorový rozmer.
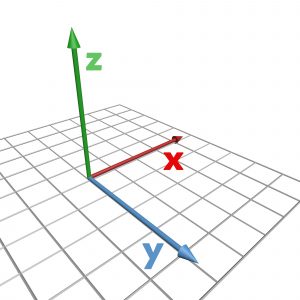
Karteziánsku sústavu súradníc nemusíme dlho predstavovať. V trojrozmernom priestore máme tri osi súradníc. Všetky sú na seba kolmé a pretínajú sa v bode [0, 0, 0]. Pozíciu každého bodu v priestore je možné presne vyjadriť pomocou troch súradníc X, Y a Z. No nič nám nebráni v dopísaní štvrtej, piatej alebo ľubovoľnej ďalšej súradnice k údajom o danom bode.
Štvorrozmerná tabuľka
Súradnice stredu štvorrozmerného priestoru sú [0, 0, 0, 0] a všetky štyri osi súradníc sú na seba kolmé. V troch rozmeroch si to nedokážeme vizualizovať, ale všetky matematické operácie naozaj sedia. Každá z osí prechádza stredom a pokračuje cez všetky body s ľubovoľným číslom na danom mieste súradnice, t. j. os X tvoria body [X, 0, 0, 0] a podobne. Štyri súradnice bodu opisujú všetky jeho vlastnosti, ktoré potrebujeme na zistenie jeho aktuálneho stavu. V štvorrozmernom priestore je to práve pozícia bodu, no v príkladoch z reálneho života to môže byť čokoľvek.
Ak ste niekedy vytvárali databázu v rôznych tabuľkových editoroch, tak sa vám možno stalo, že vám nestačilo dané pole a museli ste údaje zapisovať pomocou viacerých prepojených tabuliek. Názornou ukážkou môže byť jednoduchý zoznam ľudí, kde každý ďalší stĺpec vyjadruje napríklad ich adresu, mesto, telefónne číslo či preferované jedlo. Keď však potrebujete databázu rozšíriť a pre každé mesto zapisovať napríklad aj mestskú časť a iné údaje týkajúce sa mesta, budete musieť pridávať mnoho stĺpcov, až sa dvojrozmerná tabuľka stane neprehľadnou. Šikovnejšia by bola možnosť pridať pre mesto údaj do tretieho rozmeru, akoby do bunky tabuľky smerujúcej von z obrazovky. Rovnako by to mohlo byť aj pre všetky ostatné bunky, kde potrebujete zapísať viac údajov, ktoré spolu súvisia. Túto predstavu sa pokúste rozšíriť o ďalšiu úroveň a pre každý takýto súvisiaci údaj viacerých možných stavov sa tabuľka rozšíri do štvrtého rozmeru. Každá bunka štvorrozmernej tabuľky by mala súradnice presne popisujúce aktuálne informácie. Napríklad v druhom riadku obyvateľ menom Stanislav, v piatom stĺpci zapísané mesto Kežmarok, v treťom rozmere tabuľky zapísaná mestská časť a vo štvrtom konkrétna budova. Súradnice tabuľky, napríklad [2, 5, 1, 7] jednoznačne vyjadrujú túto informáciu bez potreby prehľadávať mnoho stĺpcov štandardnej tabuľky.
Priemety
Rám obrazu má zvyčajne obdĺžnikový tvar. Keď naň zasvietime z väčšej diaľky, aby sme docielili kolmé svetlo a nie rozptýlené, na stene sa objaví tieň. Pokiaľ rám držíme pred stenou priamo, z tvaru tieňa je možné predpokladať tvar pôvodného objektu. Keď však rám pootočíme, prípadne umiestnime až úplne ležmo vzhľadom na svetlo, na stene sa objaví iba jedna tenká línia. Takéto presvecovanie trojrozmerných objektov na dvojrozmernú stenu sa nazýva premietanie.
Kocka umiestnená presne pred svetlom nám na stene vytvorí presný štvorec. Pokiaľ však kocku rôzne otáčame, na stene budú postupne vznikať rôzne mnohouholníky. Keby sme nevedeli, aký je pôvodný presvecovaný objekt, premenlivé tvary tieňa by mohli pôsobiť veľmi neočakávane a pôvodný objekt by sme uhádli s miernymi problémami.
Zaujímavý je aj priemet gule. Nech ju už otáčame akokoľvek, tieň bude mať vždy identický tvar kruhu. Z tieňa teda nebude nijako možné zistiť, že pôvodný objekt vykonával takýto pohyb.
Pri istých uhloch a tvaroch objektov sa stráca mnoho informácií o stave pôvodných objektov. Úplne oklamať nás môže aj priemet ihlanu, ktorý je otočený dolnou stenou k svetlu. Jeho tieň bude mať tvar štvorca a na základe predošlých príkladov ľahko urobíme nesprávny predpoklad o pôvodnom objekte v tvare kocky.
Text a foto Stanislav Griguš
Fakulta matematiky, fyziky a informatiky
Univerzita Komenského v Bratislave
Videá autora nájdete na YouTube kanáli To ako prečo?.
