Buffonova ihla sa možno nepreslávila tak ako Schrödingerova mačka, Newtonova kolíska alebo Faradayova klietka – ide však o nemenej zaujímavý fenomén, ktorý pekne spája dve rôzne disciplíny – pravdepodobnosť a geometriu.
Pochádza z 18. storočia, keď sa francúzsky vedec Georges Louis Leclerc de Buffon zamýšľal nad tým, čo sa deje, keď hádžeme veľké množstvo ihiel na pásikavý papier.
Problém
Predstavme si, že máme veľký kus papiera a nakreslíme naň množstvo tenkých dlhých rovnobežných čiar s rozostupmi dĺžky 1. Predstavme si tiež, že máme k dispozícii ihlu, ktorej dĺžka je 1/2, a len tak náhodne ju pohodíme na náš papier. Otázka znie: Aká je pravdepodobnosť, že táto ihla bude po dopade pretínať niektorú z nakreslených čiar? Inak povedané, ak takto náhodne pohádžem množstvo ihiel, aký je pomer tých, ktoré pretnú niektorú čiaru, k celkovému počtu ihiel? Odpoveď je tak trochu prekvapivá: 1/π. Áno, presne to π (pí), ktoré poznáme z prostredia kruhov a kružníc. Ako je to možné?
Buffonove ihly a slíže
Francúzsky astronóm a matematik Joseph-Émile Barbier v roku 1860 našiel veľmi jednoduchý a elegantný dôkaz, ktorý navyše veľmi jasne ilustruje, ako sem to pí zo svojej vzdialenej geometrickej ríše doputovalo. Ako prvý krok je dôležité si uvedomiť, že keď je naša ihla krátka, pravdepodobnosť, že pretne čiaru, je to isté ako priemerný počet (nazvime ho P) pretnutí ihly a čiary pri pohodení veľkého počtu ihiel. Keďže počet pretnutí ihly s čiarou môže byť iba 0 alebo 1, obidve množstvá sú len vyjadrením toho istého zlomku – počet ihiel, ktoré pretínajú nejakú čiaru/počet všetkých ihiel –, ktorý dostaneme, ak začneme náhodne rozsýpať veľké množstvo ihiel na náš papier.
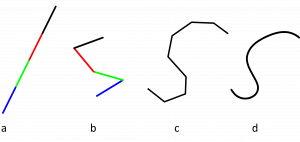
Predstavme si, že našu ihlu rozdelíme na menšie časti, ktoré rôzne ofarbíme. Ak teraz zrátame priemerný počet pretnutí modrej časti a niektorej čiary, následne priemerný počet pretnutí zelenej časti a niektorej čiary atď., a všetky sčítame, dostaneme presne P. Lenže napríklad pri sústredení sa na to, koľkokrát pretne modrá časť nejakú čiaru, je úplne nepodstatné, ako vyzerajú ostatné farebné časti ihly, ako aj ich orientácia. Rovnaký výsledok preto dostaneme, ak vezmeme pokrivenú ihlu.
Navyše tento argument nezávisí od toho, na koľko častí si ihlu rozdelíme. Nuž a keďže ľubovoľný slíž si vieme predstaviť ako veľmi kľukatú nalámanú ihlu, zisťujeme, že rovnaký výsledok P dostaneme, ak použijeme namiesto ihly ľubovoľný slíž, ktorého dĺžka je rovnaká ako pôvodná dĺžka ihly. Tento argument tiež ukazuje, že veličina P závisí lineárne od dĺžky ihly, resp. slíža – čiže ak vezmem ihlu polovičnej veľkosti, P sa zmenší na polovicu a tak podobne.
Najlepší slíž je kružnica
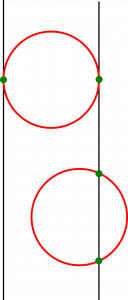
Ktorý slíž je ešte lepší ako rovný slíž? No predsa slíž-kružnica. Ak stočíme našu ihlu do kružnice, dostaneme sa do peknej a ľahko spočítateľnej situácie. Predstavme si kružnicu s priemerom 1. Nech už takúto kružnicu pohodíme hocikam, vždy pretne naše čiary práve dvakrát. Keďže táto kružnica má dĺžku π, ihle s takouto dĺžkou zodpovedá P = 2. Naša pôvodná otázka sa však týkala ihly s dĺžkou 1/2, teda 2π-krát kratšej, a preto odpoveď je 2π-krát menšia, čiže presne 1/π. Nakoniec to pí predsa len nie je až také mysteriózne.
Text a ilustrácie Fridrich Valach
University of Hertfordshire
Spojené kráľovstvo
Viac podobných článkov nájdete na stránke vedator.space.
