Difúzna rovnica bola zostavená na popis rozptyľovania sa látky v prostredí dôsledkom náhodného pohybu jej molekúl. Pretože náhodné vplyvy sa vo vede objavujú často, difúznu rovnicu nájdeme aj tam, kde by sme ju nečakali.

Napriek tomu, že zloženie hmoty z atómov bolo navrhnuté už na prelome 17. a 18. storočia, ešte na začiatku 20. storočia sa našli mnohí vedci odmietajúci ich existenciu.
Dôkaz existencie atómov a molekúl
Definitívny dôkaz priniesol až Albert Einstein vysvetlením Brownovho pohybu v jednom z článkov publikovaných vo svojom zázračnom roku 1905.
Brownov pohyb je náhodný chaotický pohyb častíc v nejakom médiu, napríklad zrniek peľu vo vode – situácia, pre ktorú bol prvý raz popísaný. A. Einstein vysvetlil Brownov pohyb ako výsledok vplyvu nárazov od veľa molekúl vody, čo vedcov presvedčilo, že na atómoch a molekulách niečo bude. Kým jedno peľové zrnko sa pohybuje náhodne, pre veľa zrniečok možno definovať ich hustotu ako počet zrniek v jednotkovom objeme, a tá sa v čase mení podľa jednoduchej rovnice nazývanej difúzna rovnica. Táto rovnica totiž popisuje difúziu, teda postupné rozptyľovanie sa pôvodne koncentrovanej látky do prostredia, napríklad parfumu vo vzduchu.
Spod mikroskopu na Wall Street
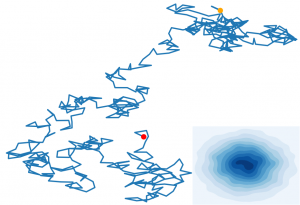
V podobnom čase ako A. Einstein aj Louis Bachelier, doktorand na parížskej Sorbonne, pracoval na matematickom popise difúzie a našiel jej iné, prekvapivé uplatnenie. Uvedomil si, že pohyby cien na burze možno považovať za náhodné, teda spĺňajúce podobné rovnice ako pri Brownovom pohybe. Bachelierova idea sa však neujala okamžite a na vzkriesenie musela počkať niekoľko desaťročí. Ako prvý sa o to zaslúžil svojrázny matematik Ed Oakley Thorp, známy svojimi dobrodružstvami v kasínach – vymyslel metódu počítania kariet v hre blackjack a tiež skonštruoval skrytý prenosný počítač predpovedajúci výsledky rulety. Osmelený výhrami sa presunul do najväčšieho kasína na svete, na Wall Street. Tam sa mu darilo zarábať aj vďaka rovnici, ktorá mu umožnila predpovedať optimálne hodnoty, ku ktorým sa postupne dostanú ceny finančných derivátov. E. O. Thorp sa z akademického sveta plne presunul do finančného a dôsledné odvodenie a publikovanie tohto modelu naceňovania derivátov počkalo na ekonómov Fishera Blacka a Myrtona Scholesa. Napriek tomu, že Blackov-Scholesov model si vyslúžil kritiku za neplatnosť svojich predpokladov a používanie modelu mimo hraníc platnosti pravdepodobne prispelo k finančným krízam, odštartoval kvantitatívny matematický prístup k investovaniu a M. Scholes zaň dostal Nobelovu cenu za ekonómiu v roku 1997. (Black sa ocenenia nedožil.)
Kvantové presahy
Základná rovnica kvantovej mechaniky, Schrödingerova rovnica, sa typicky označuje za vlnovú rovnicu. Napriek tomu, že má vlnové riešenia, Schrödingerova rovnica svojimi členmi pripomína viac difúznu rovnicu (konkrétne: obsahuje prvú časovú deriváciu a nie druhú). Líši sa však od nej v malom detaile, ktorým je prítomnosť imaginárnej jednotky i, teda čísla, ktorého druhá mocnina je -1. Schrödingerova rovnica tak zodpovedá difúznej rovnici s imaginárnym koeficientom difúzie alebo alternatívne difúznej rovnici v imaginárnom čase. Táto podobnosť nie je len kuriozitou. Motivovala vývoj výpočtových metód, ktoré k riešeniu Schrödingerovej rovnice pristupujú ako k simulácii difúzie akýchsi imaginárnych častíc. Pretože takáto simulácia dokáže nájsť riešenie Schrödingerovej rovnice veľmi presne, patrí medzi populárne metódy v kvantovej fyzike a chémii. Podobnosť s difúznou rovnicou tiež inšpirovala niektoré interpretácie kvantovej mechaniky.
Text a ilustrácia Lukáš Konečný
Univerzita v Tromsø, Nórsko
Viac podobných článkov nájdete na stránke vedator.space.