Ľudí odjakživa fascinujú geometrické vzory, či už v umení, architektúre, alebo prírode. V matematike existujú špeciálne druhy vzorov, ktoré sú výnimočné tým, že sa nikdy neopakujú. Tieto vzory, známe ako neperiodické pokrytie alebo dláždenie, sa stali svetoznámymi najmä vďaka práci matematika Rogera Penrosa.
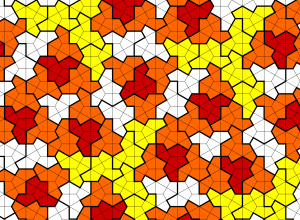
Roger Penrose v 70. rokoch minulého storočia objavil súbor jednoduchých tvarov, ktoré možno usporiadať tak, aby vytvorili zložité vzory bez akéhokoľvek opakovania sa. Predstavujú úžasný príklad toho, ako matematika dokáže objasniť a opísať zdanlivo chaotické systémy.
Neperiodické pokrytie je také, ktoré nie je možné zobraziť presne na samé seba pri žiadnom posunutí. Kde-tu sa prirodzene časti vzoru opakujú, ale ako celok je unikátny a neopakujúci sa. Takéto pokrytia, ktoré sa zdanlivo opakujú, ale v skutočnosti sa neopakujú, sa nazývajú aj kváziperiodické. Vzor je vždy vytvorený pomocou konečného počtu základných dlaždíc.
Kepler a symetrie
Už nemecký astronóm a matematik Johannes Kepler (1571 – 1630) sa zaoberal otázkou, prečo snehové vločky tvoria krásne vzory práve v tvaroch šesťuholníkov. Neexistovali ešte teórie o samousporiadaní atómov a molekúl do kryštálových štruktúr, no J. Kepler bol na tej správnej ceste. Predpokladal najmenšie čiastočky hmoty guľovitého tvaru a ich prirodzené mechanické usporiadanie do pravidelných šesťuholníkov. Podobné zadanie totiž riešil, keď dostal za úlohu vymyslieť ideálny spôsob prepravy delostreleckých gulí v lodiach tak, aby zaberali čo najmenej miesta (pozri Quark 9/2022).
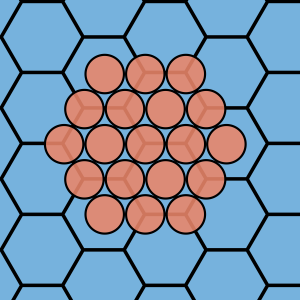
Kepler vedel aj to, že šesťuholníky dokážu pokryť plochu dokonale bez medzier. Hovorí sa tomu aj periodické pokrytie, pretože plochu dokážeme daným tvarom pokryť celú bez medzier iba jeho posúvaním bez otáčania a deformovania. Tieto pokrytia môžu byť symetrické po rotácii. Pokrytie tvorené iba štvorcami môžeme štyrikrát otočiť o 90 stupňov a bude presne sedieť na samé seba – nazýva sa aj štvoritá symetria. Kosoštvorec má dvojitú symetriu, pretože po pokrytí plochy existujú iba dve pozície po otočení o 180 stupňov. Rovnostranný trojuholník má trojitú symetriu a šesťuholník šesťnásobnú. To sú všetky takéto symetrie, ktoré existujú. To však Keplera nezastavilo a pokúšal sa hľadať iné symetrie. Nikdy sa mu ich nepodarilo nájsť.
Neperiodické pokrytie
Neperiodické pokrytie nemožno prekryť na samé seba. Vytvoríme ho veľmi jednoducho z prvotného periodického pokrytia iba štvorcami, ktoré sú uhlopriečne vždy rovnako rozdelené na dva rovnaké trojuholníky. Stačí jeden zo štvorcov otočiť o 180 stupňov. Takýchto príkladov je možné vymyslieť mnoho. Ťažšia otázka však je, či existuje množina útvarov, ktoré dokážu plochu pokryť iba neperiodicky. Znie to na prvý pohľad ako nemožná úloha: nájsť konečný počet útvarov pokrývajúcich plochu vzorom, ktorý sa nebude nikdy opakovať. A nájsť čo najmenšiu skupinu takýchto útvarov je tá pravá výzva pre matematikov.
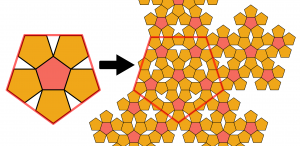
Čínsko-americký matematik Hao Wang (1921 – 1995) vytvoril skupinu 13 rôznofarebných štvorcov, ktoré sa pri ukladaní nesmú otáčať ani prevracať a musia sa k sebe prikladať vždy iba dotykom rovnakej farby. Jeho predpoklad bol však opačný: ak dokážu útvary pokryť plochu, vždy to bude periodicky. Bol to jeho študent Robert Burger, ktorý našiel množinu 20 426 rôznofarebných štvorcov pokrývajúcich plochu vždy iba neperiodicky. Postupne sa objavovali nové množiny s podstatne menším počtom útvarov. Najprv sa číslo znížilo na 104, následne na 92. V roku 1969 americký matematik Raphael Mitchel Robinson (1911 – 1995) našiel množinu iba šiestich takýchto útvarov. Následne v roku 1974 objavil množinu iba dvoch útvarov spĺňajúcich podmienku britský matematik Roger Penrose.
Text, foto a ilustrácie Stanislav Griguš
Fakulta matematiky, fyziky a informatiky
Univerzita Komenského v Bratislave
Videá autora nájdete na YouTube kanáli bit.ly/ToAkoPreco.






