Jazyk matematiky

Už matematici dávnych čias potrebovali rôzne nástroje na zápisy svojich myšlienok. Prvotná reprezentácia čohokoľvek v matematike sa musí uchopiť zapísaním čísel. Ich evolúcia v mnohých civilizáciách sveta je rôznorodá, ale zároveň v mnohom podobná.

Zápisy základných operátorov medzi číslami (plus, mínus, krát, delené) prišli až omnoho neskôr. Vedeckí intelektuáli Rímskej ríše používali latinčinu ako dorozumievací jazyk, aj ako jazyk matematiky. Všetky myšlienky však interpretovali iba slovne. Už zápis jednoduchého súčtu ako 5 + 7 = 12 zapísali Päť sčítané so sedem sa rovná dvanásť. Takáto podoba matematiky sa nazýva rétorická algebra. Komplikované rovnice a výpočty tak zaberali aj niekoľko strán písaného textu namiesto dvoch riadkov vzorcov zapísaných v súčasnej podobe.

Nula

Grécki a rímski učenci, ktorí milovali zavádzanie nových čísel a znakov, dlho nemali pomenovanie ani znak pre číslo nula. Vynájdenie nuly sa často považuje za jeden z najdôležitejších objavov v matematike. Bola to veľmi abstraktná myšlienka symbolu pre koncept ničoho, ktorá odštartovala mnoho ďalších dôležitých konceptov a objavov. Prvýkrát sa o nule hovorí v indických manuskriptoch Bakhshali datovaných do obdobia rokov 224 až 383. Ako symbol pre nulu bola použitá malá bodka nazývaná shunya-bindu s doslovným prekladom bod prázdneho miesta.
Nula sa následne dostala medzi učencov celého sveta. Najprv sa však nepovažovala za číslo, ale skôr ako znak pre prázdno. V arabskom svete vznikli súčasné podoby číslic, ako ich poznáme (pozri Quark 6/2021). Znak pre prázdno nazývali zephirum, tiež ako pomenovanie pre prázdnotu. Do Európy nulu priniesol taliansky matematik Leonardo Pisano Fibonacci (1170 – 1240). Postupne sa myšlienkovo pretransformovala a bola prijatá ako jedna z adekvátnych číslic.
Následne mohla vzniknúť aritmetika nového systému zápisu väčších čísel použitím nuly, napríklad pri číslach 10, 100, 1 000. Pre nás úplná samozrejmosť, no bol to komplikovaný koncept prijatia matematikmi, ktorí dlhé storočia používali špeciálne iné samostatné symboly pre každé väčšie číslo. Používaním nuly sa zápis veľmi zefektívnil.

Rovná sa a plus

V 16. storočí bol matematik Robert Recorde (1512 – 1558) z anglického Walesu frustrovaný neustálym písaním často opakovanej frázy rovná sa v rovniciach. V textoch ju vymenil za dve krátke rovnaké horizontálne čiary, pretože ich vnímal ako niečo najväčšmi reprezentujúce úplnú totožnosť. Mohol pokojne použiť tri čiary alebo dve vertikálne, rozhodol sa však pre horizontálne. V iných častiach sveta matematici nezávisle od neho začali používať práve dve vertikálne čiary ako znak pre rovnosť. Postupom času sa však medzi vedcami ujali dve horizontálne čiary, ktoré používame doteraz.
Znak pre plus má podobný príbeh. Najprv bol súčet reprezentovaný latinským symbolom &, nazývaným aj ampersand, ktorý označuje spojku a. Matematici chceli opäť ušetriť čas a z daného symbolu vybrali iba pravú dolnú časť. Takéto zápisy matematických myšlienok pomocou znakov sa nazývajú symbolická algebra. Cesta k nej však bola postupná a dlhá.

Symbolická algebra

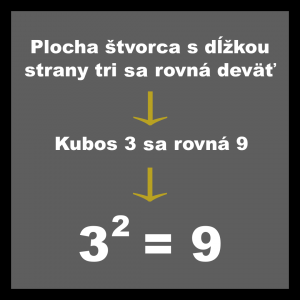
Pomocou druhej mocniny čísla je možné vypočítať obsah štvorca s danou dĺžkou strany. Napríklad štvorec s dĺžkou strany 3 cm má obsah 9 cm², pretože tri na druhú sa rovná 9 – v súčasnosti zapisujeme 3² = 9. Pre toto vyjadrenie sa dlho používalo latinské označenie štvorca kubos, zapisovali ho ako Kubos 3 sa rovná 9. Takýto zápis je na pomedzí medzi rétorickou a symbolickou algebrou. Namiesto dlhšieho opisu štvorca v zápise vyjadrenia sa používalo iba jedno slovo. Ešte vždy to však boli slovné vyjadrenia.
Transformácia z rétorickej algebry sa diala veľmi nekonzistentne medzi matematikmi po celom svete. Trvalo desaťročia, kým sa daná operácia poriadne zadefinovala a bol k nej jednoznačne priradený symbol, resp. celosvetovo jednotný grafický zápis.

Kvadratické rovnice

Premenná v rovniciach sa označovala rôzne, v dávnejšej minulosti v Indii pomocou rôznych farieb. Myšlienka nahradenia neznámeho čísla v rovnici písmenkom a počítanie s ním, akoby to bolo číslo, pochádza od francúzskeho matematika Françoisa Vièta (1540 – 1603). To dalo rozmach mnohým novým oblastiam matematiky. Zrazu bolo možné vypočítať neznáme parametre novými postupmi.

Taliansky matematik Gerolamo Cardano (1501 – 1576) vo svojom diele Ars magna z roku 1545 riešil kvadratické rovnice rôznymi spôsobmi. Nemal rád nulu, neexistovala jednoznačná predstava o záporných číslach a nemal ešte znak pre rovná sa. V škole sa v súčasnosti učí pomerne jednoduchý vzorec na výpočet neznámej v kvadratickej rovnici. G. Cardano bol však obmedzený neexistujúcimi symbolmi a tak boli jeho riešenia veľmi komplikované. Kvadratické rovnice, ktoré teraz považujeme za rovnaké, boli pre neho dve rôzne. Napríklad nedokázal číslo alebo premennú presunúť na druhú stranu rovnice.
Vo svojom diele bol však Cardano prvý, ktorý aj napriek tomu dokázal zadefinovať postupy riešenia všetkých typov kvadratických rovníc. Používal na to najmä grafické znázornenia štvorcov a geometriu. Štvorce správne poukladal a následne presúval podľa potreby rovnice.

Zložitejšie zápisy

Pre rovnice vyššieho rádu sa používal počet bodiek nad premennou. Až francúzsky filozof René Descartes (1596 – 1650) zaviedol označenie exponentu, ako ho poznáme – menšie číslo vpravo hore pri danom čísle alebo premennej. Myšlienkovo však trvalo ešte oveľa dlhšie, kým bol tretí exponent spojený s predstavou kocky a vyššie exponenty s predstavou vyšších priestorových rozmerov. Namiesto toho sa tieto vyššie exponenty definovali a riešili pomocou vlastností, vzájomných súvislostí a dvojrozmerných kriviek.
Po postupnom zjednotení a vyjadrení základných symbolov a po väčšom prepojení sveta, napríklad vďaka lodnej doprave, sa zaviedli aj symboly pre zložitejšie matematické operácie. Dôvodom pre všetky bolo najmä zefektívnenie vyjadrovania. Pre operáciu faktoriál bol zavedený výkričník a tak zápis 5 × 4 × 3 × 2 × 1 môžeme zapísať ako 5!
Zlomky chápané ako menšia časť celku sa datujú až do starovekého Egypta. Moderný zápis zlomkov ako jedno číslo nad druhým zaviedli v Indii, najprv bez horizontálnej deliacej čiary. Cesta od zlomkov k desatinným číslam či k iracionálnym a imaginárnym číslam bola však ešte veľmi dlhá.

Nekonečno

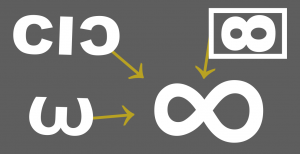
Anglický matematik John Wallis (1616 – 1703) začal pre nekonečno používať známy symbol ležatej osmičky. Doteraz jeho voľba nie je úplne jasná. Jedna z možností je, že vychádzal z dávnejšieho zápisu čísla 100 miliónov, ktoré sa zapisovalo podobným symbolom, ale ešte uzavretom v obdĺžniku. Môže to byť aj variácia označenia pre číslo tisíc, ktoré zapisovali ako písmeno C, písmeno I a následne zrkadlovo otočené C. Tiež grécky symbol omega, často reprezentujúci koniec v rôznych zmysloch, nápadne pripomína ležatú osmičku.
Nekonečno je pekným príkladom zavŕšenia symbolickej algebry. Je to dôkaz toho, že vieme symbolmi zapísať aj niečo, čo si nedokážeme plne predstaviť.

Text a foto Stanislav Griguš
Fakulta matematiky, fyziky a informatiky
Univerzita Komenského v Bratislave
Videá autora nájdete na YouTube kanáli To ako prečo?