Čo všetko dokážeme iba pomocou obyčajného kružidla a pravítka? Túto zdanlivo nevinnú otázku si kedysi položili starovekí Gréci. Zaviedla ich vtedy do ďalekých a dovtedy nezmapovaných zákutí matematiky. Niektoré z nich nie sú úplne prebádané ani v súčasnosti.

Mnohí si zo školy pamätáme, ako sme pomocou pravítka a kružidla riešili rôzne geometrické úlohy. Napríklad ako skonštruovať kolmicu na danú priamku alebo ako zostrojiť trojuholník so stranami dlhými 3, 4 a 5 centimetrov.
Mnohouholníky
Predstavme si, že máme namiesto pravítka k dispozícii iba obyčajnú dlhú a rovnú dosku bez akýchkoľvek vyznačených dielikov. Inak povedané, jediné, na čo môžeme toto pravítko použiť, je vytvorenie priamej čiary prechádzajúcej dvoma bodmi. Pre úplnosť dodám, že pri týchto konštrukciách ešte potrebujeme ceruzku na zakreslenie čiar a bodov.
S kružidlom a takýmto ochudobneným pravítkom máme zrazu menej možností. Napríklad spomenutý trojuholník už asi nezostrojíme, keďže si nevieme odmerať potrebné vzdialenosti. Niektoré dôležité konštrukcie sú však naďalej možné. Ak nám kamarát prichystá nejakú úsečku, sme schopní zostrojiť štvorec, ktorý bude mať túto úsečku ako jednu zo strán – použijeme pritom istý starý trik s kružidlom na nakreslenie kolmice. Keby sme vedeli kresliť body do trojrozmerného priestoru, potom poľahky dokážeme zostrojiť aj kocku s hranou danou našou úsečkou. Rovnako dobre vieme zostrojiť napríklad aj rovnostranný trojuholník, prípadne pravidelný šesťuholník. S päťuholníkom je to o niečo komplikovanejšie, ale tiež to ide. Čo však taký pravidelný sedemuholník?
Nie všetko sa dá
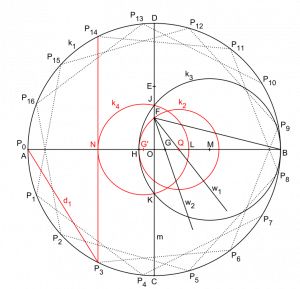
Ukazuje sa, že zostrojiť sedemuholník iba pomocou nášho pravítka a kružidla je nemožné. Rovnako nedokážeme zostrojiť pravidelný 9-uholník, 11-uholník alebo 13-uholník. Prekvapivo však vieme zostrojiť pravidelný 15- alebo 17-uholník. Ako sme k týmto číslam prišli? Odpoveď je trochu zamotaná. Z prác matematikov Carla Friedricha Gaussa a Pierra Wantzela vieme, že zostrojiteľnosť mnohouholníkov súvisí s tzv. Fermatovými prvočíslami. Koľko je samotných Fermatových prvočísel, to nevieme. Poznáme ich päť: 3, 5, 17, 257, 65 537. Doteraz však nevieme, či sú to všetky.
Gauss a Wantzel ukázali, že pravidelný N-uholník možno zostrojiť vtedy a len vtedy, keď číslo N, rozložené na súčin prvočísel, obsahuje iba dvojky a Fermatove prvočísla. Navyše, zatiaľ čo dvojok môže byť ľubovoľne veľa, každé z Fermatových prvočísel sa v tomto súčine môže vyskytnúť len raz. Z tohto dôvodu vieme zostrojiť pravidelný 15-uholník (lebo 15 = 3 × 5) alebo 68-uholník (lebo 68 = 2 × 2 × 17), ale nie 9-uholník (lebo 9 = 3 × 3 obsahuje dvakrát to isté Fermatovo prvočíslo) alebo 11-uholník (lebo 11 je prvočíslo, ale nie Fermatovo).
Prvočísla a geometria
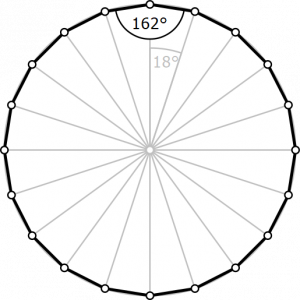
Ako Gauss a Wantzel k tomuto výsledku prišli? Detailné vysvetlenie je síce relatívne komplikované, spomeňme však aspoň jeden kľúčový medzikrok. Je ľahké vidieť, že pravidelný N-uholník vieme zostrojiť práve vtedy, keď sme schopní skonštruovať 360/N-stupňový uhol. Na skonštruovanie takého uhla zasa potrebujeme, aby sme kosínus tohto uhla dokázali zapísať iba pomocou štyroch základných aritmetických operácií a druhej odmocniny. To sú totiž jediné operácie, ktoré môžeme dosiahnuť s použitím pravítka a kružidla. Uvedení matematici potom ukázali, že kosínus si možno takto rozpísať práve vtedy, keď má číslo N už uvedený prvočíselný rozklad.
Otázka zostrojiteľnosti pravidelných mnohouholníkov teda zaujímavým a netriviálnym spôsobom súvisí s istou skupinou prvočísel. Toto pozorovanie z prelomu 18. a 19. storočia poskytuje jeden z pozoruhodných mostov medzi rôznymi matematickými disciplínami – v tomto prípade medzi teóriou čísel a geometriou.
Fridrich Valach
Imperial College London






