
Horské dráhy zrejme poznáte, niektorí ste na nejakej možno aj viezli. A možno na takej, ktorá vás previezla zvislým oblúkom. Verím, že vtedy ste nemali čas rozmýšľať nad tým, aký presný tvar oblúk mal. A tak si to premyslíme teraz.
Budeme na to potrebovať dva jednoduché poznatky. Tým prvým je skutočnosť, že vláčik na horskej dráhe nemá motor a dopredu sa pohybuje len pôsobením gravitačnej sily. Druhým je pohyb po kružnici – konkrétne to, že sa pri ňom teleso pohybuje so zrýchlením, ktoré klesá s polomerom kružnice a rastie s rýchlosťou.
Limit preťaženia
Predstavme si teda vláčik, ktorý z vodorovných koľají nabehne veľkou rýchlosťou na zvislý kružnicový oblúk. Na začiatku pasažieri pociťujú veľmi veľké zrýchlenia, ale ako vláčik stúpa, jeho rýchlosť klesá a dostredivé zrýchlenie sa zmenšuje, v najvyššom bode je najmenšie a potom zasa narastá. Po prejdení celého oblúka dostredivé zrýchlenie klesne späť na nulu.

Nejaké zrýchlenia sú na horskej dráhe v poriadku, koniec koncov pre tento zážitok tam ľudia chodia. No aj tu všetkého veľa škodí a hodnota maximálneho preťaženia, ktorú povoľujú pravidlá pre konštrukciu horských dráh (kvôli bezpečnosti a zdraviu ľudí) je 6 g, pre dlhšie časové úseky nie viac ako 4 g. Kruhové oblúky spĺňajúce tieto kritériá by boli príliš veľké, v rozumne veľkých oblúkoch by zasa preťaženia dosahovali hodnoty až 12 g.
Tvar obrátenej kvapky
Riešenie tohto problému vám možno už napadlo. Oblúk nebude kružnica, ale krivka, na ktorej sa polomer kruhového pohybu vláčika bude meniť. Na začiatku, keď má vláčik ešte veľkú rýchlosť, je krivka vcelku plochá. Postupne, ako vláčik stráca rýchlosť, sa jej zakrivenie zväčšuje a pri klesaní sa krivka vyrovnáva. Dostaneme tak oblúk s tvarom podobným kvapke obrátenej smerom nahor.
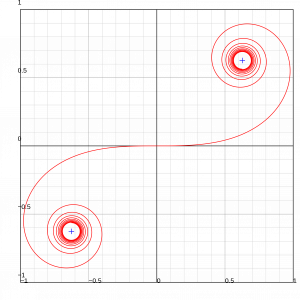
Presný tvar krivky sa dá dopočítať z veľkosti a priebehu preťaženia, ktoré chcú konštruktéri pre ľudí pripraviť – napríklad konštantných 4 g s trochou 6 g pre najextrémnejšiu možnú obrátku. Má to však drobný háčik. Všetky časti vláčika sa pohybujú rovnakou rýchlosťou – ak nie, tak to je veľký problém –, ale nachádzajú sa v rôznych častiach krivky. A to znamená, že pasažieri na začiatku, v strede a na konci vláčika pociťujú iné preťaženia. Tieto rozdiely môžu byť celkom významné a treba dávať pozor, aby bol limit 6 g splnený pre všetkých.
Eulerova špirála
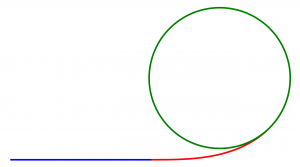
Okrem veľkých preťažení sú nepríjemné aj prudké zmeny zrýchlenia. Preto sa trate konštruujú tak, že polomer zakrivenia narastie pomaly. Na to sa využíva tzv. klotoida, teda Eulerova špirála – jej zakrivenie, čo je prevrátená hodnota uvedeného polomeru, narastá lineárne s prejdenou vzdialenosťou. Oblúk teda najskôr nasleduje klotoidu a až keď sa zrýchlenie vyšplhá na požadovanú hodnotu, prejde do tvaru kvapky: preťaženie narastá príjemne a ľudia majú z oblúka oveľa lepší zážitok.
Na ideu špirály prišlo viac ľudí nezávisle. Používa sa napríklad pri konštruovaní ciest pre tvar zákrut, pretože v jednoduchej kruhovej zákrute by sme museli volantom auta náhle trhnúť, čo nie je ani bezpečné, ani príjemné. Z úplne iných dôvodov sa Eulerova krivka objavuje aj pri výpočtoch ohybu svetla a iných vĺn na prekážkach. A tak nakoniec oblúky na horských dráhach spájajú difrakciu svetla s konštrukciou ciest.
Juraj Tekel
Fakulta matematiky, fyziky a informatiky
Univerzita Komenského v Bratislave
Viac podobných článkov nájdete na stránke vedator.space.






