Štyri štvorky

Matematické hry často na prvý pohľad nedávajú zmysel, no vždy sa za nimi skrýva tá pravá krása matematiky. Cieľom hry Štyri štvorky (z ang. Four fours) je vytvoriť čo najviac kladných celých čísel použitím iba štyroch štvoriek v kombinácii s matematickými operáciami.

Pravidlom je použitie vždy všetkých štyroch štvoriek a neobmedzené množstvo operácií. V prvej úrovni hry je dovolené použiť operácie sčítanie (+), odčítanie (-), násobenie (×), delenie (/) a zátvorky (). Začiatok s číslom nula je veľmi ľahký: 4 + 4 – 4 – 4 = 0. Následne sa bez problémov dostaneme k číslu 9. Môžete si to skúsiť.

Pokročilá aritmetika

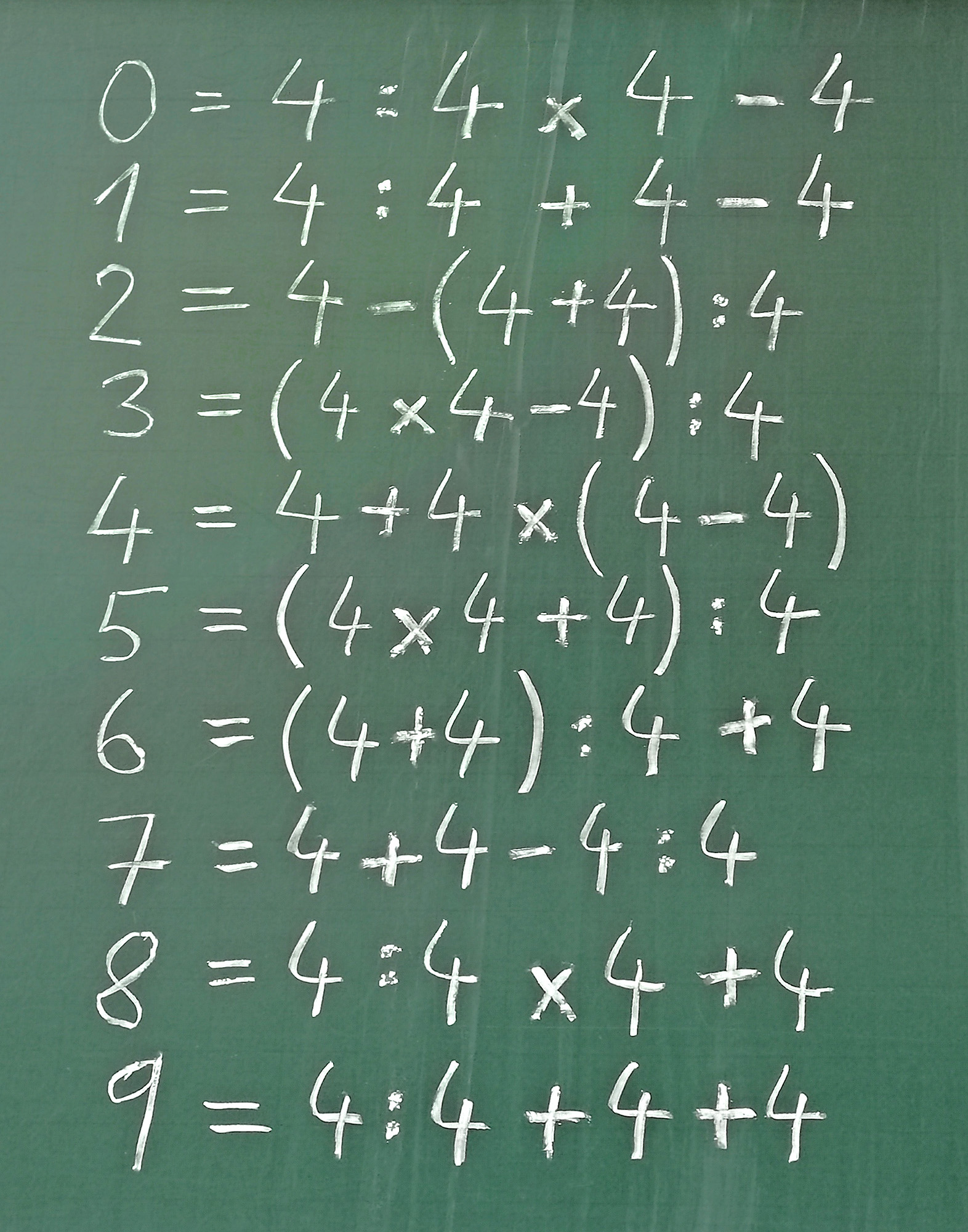
Pre pokračovanie k získaniu vyšších čísel je potrebné zaviesť matematické operácie, ktoré nie sú úplne bežné. Prvou z nich je tzv. zreťazenie, operácia, pri ktorej sa dve čísla spoja do jedného spôsobom priamo naviazania jednotlivých číslic. Vznikne tak možnosť použiť v hre čísla 44 alebo 444. Ďalej je to pridanie desatinnej čiarky na ľubovoľné miesto, čím dostaneme čísla 4,4 alebo 0,4 (tu je použitá aj cifra 0, no v matematike sa číslo 0,4 môže korektne napísať aj ako ,4 bez použitia cifry 0). Potrebná je aj operácia s názvom faktoriál, ktorá sa označuje výkričníkom a znamená súčin všetkých kladných celých čísel zostupne od daného čísla až po číslo 1. Napríklad, 4! = 4 × 3 × 2 × 1 = 24. Ďalšou operáciou je exponovanie, ktoré umocňuje čísla: 4⁴ = 4 × 4 × 4 × 4 = 256. Opakom mocniny je odmocnina. Jej výsledkom je číslo, ktoré je potrebné vynásobiť, aby sme dostali číslo pod odmocninou. Druhá odmocnina čísla 4 je číslo 2, pretože 2² = 2 × 2 = 4. Tretia odmocnina čísla 64 je číslo 4, pretože 4³ = 4 × 4 × 4 = 64.
Mnohí matematici dokážu zájsť postupne až po číslo 500 a viac. Konštruujú pritom rôzne ďalšie matematické operácie, či už kombinatorické zápisy alebo trojuholníkové čísla. Pekným príkladom je číslo 99.

Prvé dve štvorky použijeme ako vyjadrenie počtu prvkov štyri zo štyroch v zmysle percentuálneho vyjadrenia. Dostaneme sto percent, takže číslo 100. Potom odpočítame jednotku ako delenie štvorky štvorkou, zapíšeme: [4/4]% – 4/4.

Ako ďaleko sa dá zájsť?

Pre úplnosť si musíme predstaviť ešte jednu matematickú operáciu, a to logaritmus.
Ak platí a = b^c, tak logaritmus čísla a pri základe b sa rovná číslu c, log_ba = c. Spresnime si ešte, že druhú odmocninu čísla možno vyjadriť aj ako číslo umocnené na ½. Teraz si poriadne zahrejeme mozgové bunky a vytvoríme peknú postupnosť s použitím iba dvoch štvoriek, logaritmu a odmocniny. Logaritmus pri základe 4 odmocniny zo štyroch sa rovná jednej polovici, teda log₄√4 = ½. Postupne pridávame odmocniny a dostaneme log₄√√4 = ¼, potom log₄√√√4 = ⅛ a tak ďalej. Získali sme postupnosť klesajúcich zlomkov a tá sa dá obrátiť opäť pomocou logaritmu na postupnosť stúpajúcich čísel.

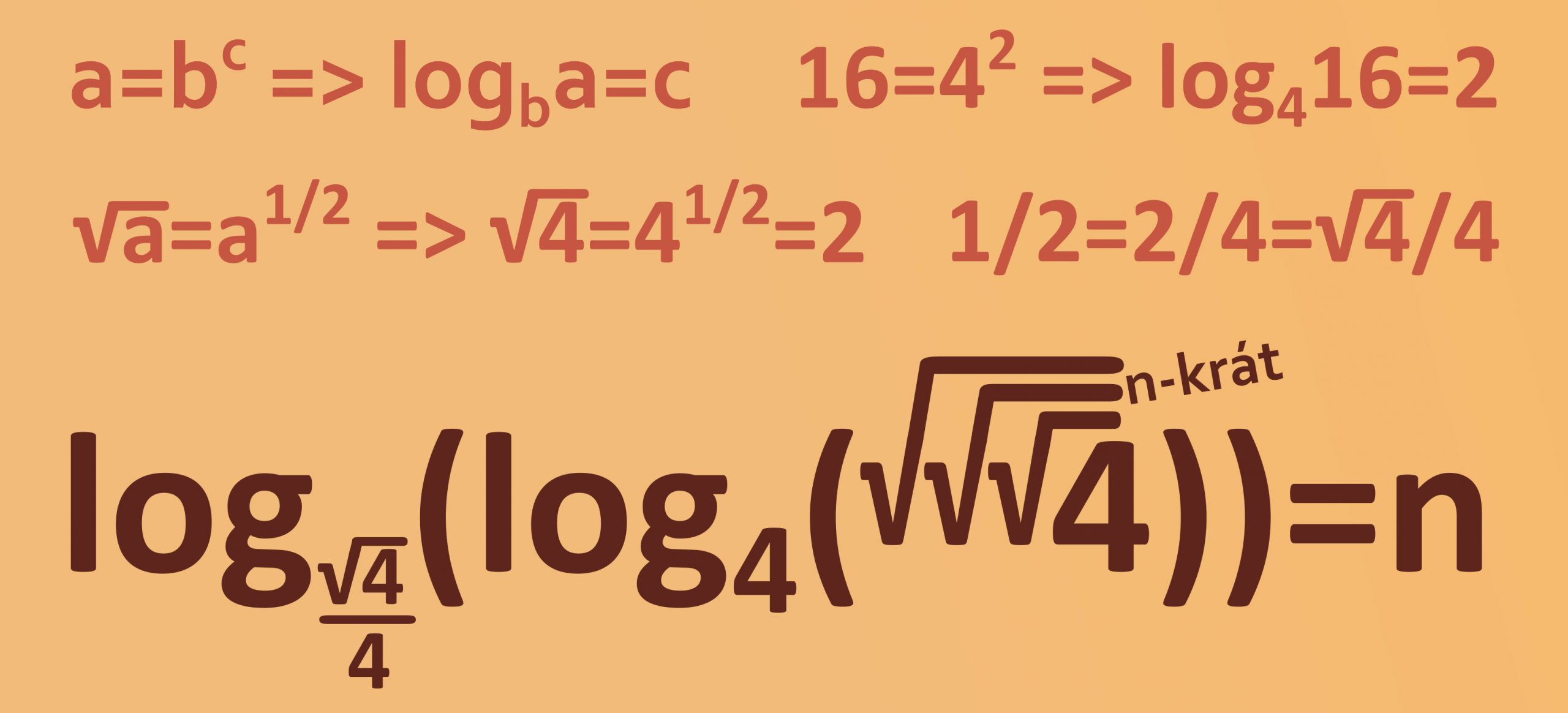
Logaritmus ½ pri základe ½ sa rovná 1, ¼ sa rovná 2, ⅛ sa rovná 3. Číslo ½ dokážeme ľahko vyjadriť pomocou dvoch štvoriek, a tak vyjadríme všeobecný vzorec pre všetky kladné reálne čísla použitím štyroch štvoriek a iba dvoch logaritmov. Koľko odmocnín vo vzorci použijeme, také číslo dostaneme.
Tento spôsob riešenia našiel britský teoretický fyzik a držiteľ Nobelovej ceny za fyziku Paul Dirac (1902 – 1984) v tridsiatych rokoch 20. storočia a tým vlastne celú túto hru pokazil.

Text a foto Stanislav Griguš
Fakulta matematiky, fyziky a informatiky
Univerzita Komenského v Bratislave
Videá autora nájdete na YouTube kanáli bit.ly/ToAkoPreco.