Matematika ešte nie je pripravená na tento problém, tvrdia mnohí poprední matematici a vedci po celom svete. Nikomu neodporúčajú venovať svoj výskum práve tejto problematike. Napriek tomu je zadanie problému také jednoduché a jasné, že ho bez problémov pochopia aj žiaci základnej školy.
Zvoľme si ľubovoľné kladné celé číslo. Riadiť sa budeme iba dvomi jednoduchými pravidlami. Ak je číslo párne, vydelíme ho dvomi. Ak je číslo nepárne, strojnásobíme ho a pripočítame jednotku. Pokračujeme rovnakým pravidlom, čím získame postupnosť čísel. Aká bude táto postupnosť pre ľubovoľné kladné celé číslo n? Bude rásť donekonečna alebo, naopak, bude neustále klesať? Je možné nájsť akýsi všeobecný vzorec či pravidlo, podľa ktorého sa bude postupnosť správať?
Collatzov predpoklad
Skúsme si to napríklad pre číslo 10. Je párne, takže ho vydelíme dvomi. Dostaneme nepárne číslo 5, ktoré podľa druhého pravidla strojnásobíme a pripočítame jednotku. Dostaneme číslo 16. Vydelíme ho dvomi, získame číslo 8. To opäť vydelíme dvomi na číslo 4, následne 2 a 1. Číslo 1 je nepárne, strojnásobením a pripočítaním jednotky dostaneme opäť 4. Tu sa zacyklíme donekonečna na opakujúcich sa číslach 4, 2 a 1. Môžeme si zapísať, že zvolené číslo 10 sa opakovaním krokov dostalo na číslo 1, resp. do cyklu 4, 2 a 1. Zároveň vieme, že takisto skončia aj všetky čísla, ktorými sme počas riešenia prešli, teda 5, 16 a 8.
Matematici prešli mnoho ďalších čísel. A zatiaľ sa vždy dostali do rovnakého cyklu. Vyskúšali všetky kladné celé čísla zhruba až do 268, čo je 295 147 905 179 352 825 856. Hovorí o tom známy Collatzov predpoklad: Každé kladné celé číslo touto postupnosťou dôjde k číslu 1. Lothar Collatz (1910 – 1990) bol nemecký matematik a jeho predpoklad doteraz ostal nepotvrdený. Pritom sa mu venuje naozaj mnoho matematikov, či už v oblasti kombinatoriky alebo teórie čísel. Aby sa predpoklad potvrdil, je potrebné nájsť a dokázať všeobecný vzor správania sa postupnosti krokov, ktorý bude platiť pre každé kladné celé číslo.
Strom krokov postupnosti
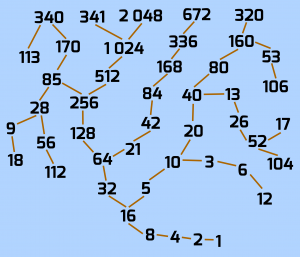
Keďže predpokladáme, že každé číslo sa dostane k číslu 1, môžeme si postupnosť zakresliť aj vo forme akéhosi stromu krokov. Pre číslo 10 už postupnosť poznáme. Najnižšie číslo, pre ktoré zatiaľ nie, je číslo 3. Po prvom kroku dostaneme hneď číslo 10, takže môžeme trojku rovno napojiť na náš strom. Rovnako z čísla 6 dostaneme ihneď trojku. Sedmička má už trochu dlhší reťazec postupnosti, ale taktiež sa dopracuje k číslu 10. Takto môžeme strom rozširovať, napájať jednotlivé vetvy postupností a skúmať ich štruktúru. Dĺžka postupností pre vyššie čísla je naozaj veľká a jednotlivé vetvy sa budú rapídne rozširovať. Pre krajšie zobrazenie tohto stromu s enormným množstvom čísel a krokov postupnosti je možné zakresliť ho aj v trojrozmernom priestore. Graf sa vetví jedným smerom pre párne číslo a iným smerom pre nepárne. Všetky celé čísla a ich postupnosti sa v priebehu krokov spájajú a stretávajú v čísle 1.
Čísla v postupnostiach rýchlo stúpajú a klesajú. Taktiež dĺžky jednotlivých postupností sú diametrálne odlišné aj pre susediace alebo veľmi blízke začiatočné celé čísla. Napríklad číslu 1 270 trvá iba 31 krokov, kým sa dostane na číslo 1, ale číslu 1 278 až 132 krokov. Skúmať môžeme aj najvyššie číslo, aké je v danej postupnosti dosiahnuté. Číslo 26 vo svojej postupnosti dosiahne maximálne číslo 40 a trvá mu 10 krokov, kým sa dostane na jednotku. Susedné číslo 27 však stúpne až na 9 232 a spolu po 111 krokoch padne na číslo 1. Tieto vlastnosti Collatzovho predpokladu je možné rôzne vizualizovať, hľadať opakujúce sa vzory, pravidlá a náčrty dôkazu. Vo všetkých týchto vlastnostiach sa nenašiel jednoznačný vzor správania sa postupnosti vo všeobecnosti, preto zatiaľ nebolo možné predpoklad potvrdiť.
Text a foto Stanislav Griguš
Fakulta matematiky, fyziky a informatiky
Univerzita Komenského v Bratislave
Videá autora nájdete na YouTube kanáli bit.ly/ToAkoPreco.
