V predchádzajúcich článkoch našej rubriky sme sa začali venovať zmene skupenstva látok a uviedli sme si, ako sa správajú pri rôznych teplotách a tlakoch. Teraz sa pozrieme na zmenu skupenstva z mikroskopického hľadiska a objasníme si správanie niektorých látok pri kontakte s inými.
Už sme si pripomenuli, že bežne poznáme tri skupenstvá látky, a to tuhé, kvapalné a plynné. Pre naše účely nebudeme uvažovať plazmu. To, v akom skupenstve sa daná látka nachádza, závisí od dvoch parametrov, teploty a tlaku. Vieme, že dodávaním tepla alebo energie nejakej látke by mala postupne rásť aj jej teplota, až dosiahne bod topenia alebo varu. Látka zmení skupenstvo a pri dodávaní tepla teplota ďalej rastie. Ukazuje sa však, že je to o trochu komplikovanejšie.
Merné skupenské teplo
Pri dosiahnutí bodu topenia alebo varu látky a dodávaní tepla pozorujeme, že teplota látky nerastie okamžite. Nastáva tak stav, keď sa teplota nemení. Teplo dodávané látke je spotrebované na zmenu skupenstva a rozbitie väzieb molekúl, ktoré látku tvoria. Až po tom, čo sa látka rozpustí alebo vyparí, začne teplota opätovne stúpať. Toto ďalšie teplo, ktoré je potrebné dodať látke, sa nazýva latentné teplo topenia alebo vyparovania alebo aj merné skupenské teplo. Predstavuje množstvo tepla, ktoré prijme jeden kilogram látky pri teplote topenia alebo vyparovania, aby sa celá premenila na kvapalinu, respektíve plyn. Dobre sa to dá ilustrovať predovšetkým pri práci s vodným ľadom a vodou.
Merné skupenské teplo topenia ľadu je približne 334 000 J/kg, merné skupenské teplo vyparovania vody je asi 2 257 000 J/kg. Vidíme, že ide o pomerne vysoké čísla. Znamená to, že na to, aby voda zmenila skupenstvo, je potrebné jej dodať pomerne veľa tepla. Predstavme si, že máme 100 gramov ľadu, ktoré pridáme do 800 ml vody, čo predstavuje 800 gramov vody. Aby sa týchto 100 gramov rozpustilo, potrebujeme z vody odobrať 33 400 joulov.
Usporiadanosť častíc
V predchádzajúcich článkoch sme uviedli, že konštanta popisujúca, koľko tepla je potrebné dodať látke, aby teplota jedného kilogramu tejto látky stúpla o jeden stupeň, sa nazýva hmotnostná tepelná kapacita. V prípade vody je to asi 4 219 J/(kg · K). Teplota 800 ml vody teda klesne asi o 10 °C, keď sa ľad úplne rozpustí. Môžeme teda vidieť, že voda (alebo ľad) je využiteľná ako kvalitná chladiaca látka.
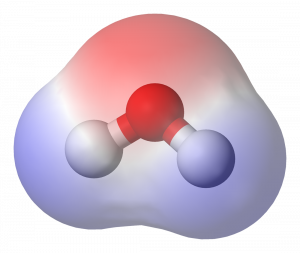
Už vieme, že skupenstvo látky predstavuje usporiadanie jej molekúl. V prípade tuhého skupenstva sú molekuly usporiadané v pevných mriežkach. Pri dodávaní energie sa začnú molekuly viac pohybovať, až sa väzby medzi nimi narušia a molekuly sa pohybujú voľnejšie. Látka tak prechádza do kvapalného skupenstva. S ďalším zvyšovaním teploty sa molekuly pohybujú voľne a vyplnia celý priestor, ktorý im je poskytnutý. Získavame tak plynné skupenstvo.
To, v akom skupenstve sa látka nachádza, závisí od vzájomného súboja medzi silou väzieb, ktoré držia molekuly pokope, a ich kinetickou energiou, ktorá ich núti sa od seba čo najviac vzdialiť. Keď sú väzby silnejšie ako kinetická energia, látka je v tuhom skupenstve. V opačnom prípade je to kvapalina až plyn.
Boltzmannova konštanta
Uvažujme teraz, aká je kinetická energia jednej takejto molekuly. Koncom 19. storočia prišiel významný rakúsky fyzik Ludwig Boltzmann (1844 – 1906) s rovnicou vyjadrujúcou kinetickú energiu alebo aj tepelnú energiu molekúl. Táto rovnica hovorí, že tepelná energia je úmerná teplote molekuly meranej v kelvinoch. Kelvinova stupnica je podobná ako Celziova, iba s tým rozdielom, že má posunutý nulový bod a nemôže ísť do záporných hodnôt. Hodnotu v kelvinoch jednoducho získame tak, že k stupňom Celzia pripočítame 273. Hodnota 0 kelvinov predstavuje absolútnu nulu a je to teplota, pri ktorej je tepelná energia molekuly nulová.
Rovnica hovorí, že tepelná energia je násobok nejakej konštanty C, konštanty kB a teploty, pričom kB je tzv. Boltzmannova konštanta a ide o univerzálnu konštantu prírody. Jej hodnota je približne 1,38 × 10-23 J/K. Konštanta C závisí od atmosférického tlaku a typu molekuly. Pri jednej atmosfére sa rovná 3/2. Pri izbovej teplote 27 °C (predstavujúc 300 K) je tak energia jednej molekuly približne 6,2 × 10-21 joulov.
Mgr. Patrik Čechvala
Fakulta matematiky, fyziky a informatiky
Univerzita Komenského v Bratislave
Foto Pixabay
