Na pulty kníhkupectiev sa dostáva prvý slovenský preklad a komentár najslávnejšej knihy s matematickým obsahom v celej histórii matematiky – Euklidovho diela s lakonickým názvom Základy (Stoicheia).
Uznávaný starogrécky učenec, mysliteľ a pedagóg Euklides pôsobil okolo roku 300 pred n. l. vo vrcholnej vedeckej a umeleckej inštitúcii vtedajších čias, v akadémii Museion, založenej a prosperujúcej v hlavnom meste egyptskej ríše Alexandrii pod záštitou panovníka Ptolemaia I. (Sotéra). Euklides v Základoch zhrnul, systematicky usporiadal, doplnil, rozvinul a didakticky majstrovským spôsobom prezentoval všetky podstatné vedecké výsledky v matematike, ku ktorým grécka veda dospela v 6. – 4. storočí pred n. l. na báze osvojenia matematických poznatkov starovekých civilizácií Stredomoria a Blízkeho východu a ich pretavenia a prekonania v duchu vlastného pokroku vo filozofii, logike a metodológii vedy. V trinástich kapitolách sú v obsahovej a logickej gradácii zachytené temer všetky originálne prínosy antickej gréckej geometrie, aritmetiky a algebry.
Propozícia 23.
Na danej priamke a v danom bode na nej zostrojte priamkový uhol rovnajúci sa danému priamkovému uhlu.
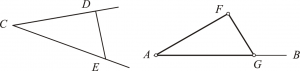Nech AB je daná priamka, A – (daný) bod na nej a DCE daný priamkový uhol. Požaduje sa zostrojiť na danej priamke AB a v danom bode A na nej priamkový uhol rovnajúci sa danému priamkovému uhlu DCE.
Nech D a E sú po poriadku ľubovoľné body na priamkach CD a CE a nech DE je ich spojnica. Nech trojuholník AFG je zostrojený z troch priamok rovnajúcich sa (po poriadku) priamkam CD, DE a CE tak, že CD sa rovná AF, CE sa rovná AG a DE sa rovná FG [prop. 1.22]. Potom, pretože dve strany DC a CE sa po poriadku rovnajú stranám FA a AG a základňa DE sa rovná základni FG, uhol DCE sa rovná uhlu FAG [prop. 1.8].
Teda priamkový uhol FAG rovnajúci sa priamkovému uhlu DCE bol zostrojený v danom bode A na danej priamke AB. – To je naozaj požiadavka, ktorú bolo treba splniť.
Propozícia 24.
Ak sa v dvoch trojuholníkoch dve strany prvého (trojuholníka) rovnajú po poriadku dvom stranám druhého (trojuholníka), ale uhol zovretý týmito stranami v prvom (trojuholníku) je väčší než uhol zovretý (zodpovedajúcimi) stranami v druhom (trojuholníku), tak aj základňa prvého (trojuholníka) je väčšia než základňa druhého (trojuholníka).
Nech ABC a DEF sú dva trojuholníky, v ktorých dve strany AB, AC sa po poriadku rovnajú dvom stranám DE, DF, t. j. AB sa rovná DE a AC sa rovná DF. Nech uhol v bode A je väčší než uhol v bode D. Tvrdím, že aj základňa BC je väčšia než základňa EF.
Vskutku, pretože uhol BAC je väčší než uhol EDF, nech je na priamke DE v jej bode D zostrojený uhol EDG rovnajúci sa uhlu BAC [prop. 1.23]. Nech DG je nanesená tak, aby sa rovnala obom rovnajúcim sa priamkam AC, DF [prop. 1.3], a nech sú vytvorené spojnice EG a FG.
Potom, pretože AB sa rovná DE a AC sa rovná DG, dve priamky BA, AC sa po poriadku rovnajú dvom priamkam ED, DG. Okrem toho aj uhol BAC sa rovná uhlu EDG. Preto aj základňa BC sa rovná základni EG [prop. 1.4].
Ďalej, pretože DF sa rovná DG, uhol DGF sa taktiež rovná uhlu DFG [prop. 1.5], preto uhol DFG je väčší než uhol EGF. A pretože trojuholník EFG má uhol EFG väčší než uhol EGF a oproti väčšiemu uhlu sa nachádza väčšia strana [prop. 1.19], je strana EG väčšia než strana EF. Ale EG sa rovná BC. Tým aj strana BC je väčšia než EF.
Teda, ak v dvoch trojuholníkoch dve strany prvého sa rovnajú po poriadku dvom stranám druhého, ale uhol zovretý týmito dvoma stranami v prvom trojuholníku je väčší než uhol zovretý dvoma zodpovedajúcimi stranami v druhom trojuholníku, je základňa v prvom trojuholníku väčšia než základňa v druhom trojuholníku. – Toto je naozaj vec, ktorú dokázať sa požadovalo.
Kniha vyšla v roku 2022 vo vydavateľstve Perfekt s podporou FPU.
Súťažná otázka
Ak nám do 30. septembra 2022 pošlete správnu odpoveď na otázku:
Ktorého geometrického tvaru sa týkajú dve Euklidove vety?
zaradíme vás do žrebovania o knihu Euklides: Základy z vydavateľstva Perfekt.
Svoje odpovede posielajte na adresu redakcie: odpovednik@quark.sk alebo Quark, Staré grunty 52, 842 44 Bratislava 4.
