Britský matematik, fyzik a inžinier William Thompson, známejší pod menom lord Kelvin, dostal v 19. storočí nápad, že rozmanitosť mikrosveta by sa dala elegantne vysvetliť, keby sme predpokladali, že atómy zodpovedajú uzlom v éteri (látke, o ktorej sa vtedy predpokladalo, že je všadeprítomná). Existuje mnoho rôznych uzlov, a to by zodpovedalo pestrej palete rozličných atómov a ich vlastností.
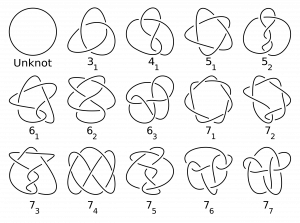
Jeho kolega, škótsky fyzik Peter Tait, sa preto rozhodol venovať systematickému štúdiu uzlov – a výsledkom bola prvá tabuľka uzlov. Myšlienku éteru síce krátko na to opustili, teória uzlov však pokračovala a v súčasnosti je z nej významná matematická disciplína.
Nie sú uzly ako uzly
V prvom rade treba povedať, že keď hovoríme o uzloch, máme na mysli uzavreté uzly, čiže akési zmotania pomyselného povrázku, ktoré majú zlepený začiatok a koniec; prípadne si predstavme stočenú gumičku. Medzi najjednoduchšie uzly patria trojlístkový alebo osmičkový uzol (na obrázku sú označené ako 31 a 41).
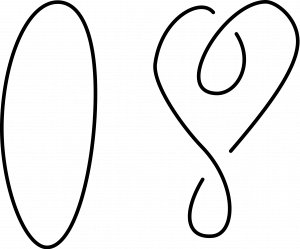
Niekedy sa môže stať, že dva uzly, ktoré na prvý pohľad vyzerajú rôzne, sa v skutočnosti dajú prepliesť (bez použitia nožníc) jeden na druhý; ide teda o ten istý uzol. Jednoduchý príklad je na ďalšom obrázku, kde obyčajným pretočením možno prerobiť situáciu vpravo na nezatočenú slučku vľavo (takáto prostá slučka sa tiež považuje za uzol, podobne ako sa nula považuje za číslo).
Ako ich rozlíšiť?
Vo všeobecnosti je otázka Kedy sú dva uzly rovnaké? veľmi komplikovaná. Napríklad pri tzv. Perkovom páre sa dlho myslelo, že ide o dva rôzne uzly, až kým v roku 1973 americký matematik Kenneth Perko neukázal, že ide o jeden a ten istý.
Na rozlišovanie uzlov sa v matematike používajú tzv. invarianty. Ide o vlastnosť, ktorú možno prideliť ľubovoľnému uzlu. Ak majú dva uzly túto vlastnosť rozdielnu, vieme s istotou povedať, že ide o rozdielne uzly. Nanešťastie, ak majú dva uzly túto vlastnosť rovnakú, vo všeobecnosti z toho neplynie, že sú rovnaké – vtedy je nutné skúmať inú vlastnosť, prípadne skúsiť ukázať, že jeden uzol možno prerobiť na druhý.

Trojofarbiteľnosť
Pekným príkladom uzlového invariantu je tzv. trojofarbiteľnosť (po ang. tricolorability). Na to, aby sme zistili, či je daný uzol trojofarbiteľný, postupujeme takto: Najprv si daný uzol nakreslíme na papier, resp. ho premietneme do roviny (podobne ako na obrázkoch). Pri tomto priemete natrafíme na niekoľko bodov, kde sa vlákna krížia – spodné vlákno si vtedy nakreslíme prerušene. Následne skúsime jednotlivé úseky (t. j. neprerušené úseky vlákna) vyfarbiť, a to tak, aby sme splnili dve podmienky: 1. Musíme použiť práve tri rôzne farby. 2. Pri každom bode, kde sa vlákna krížia, sa na obrázku stretávajú tri úseky uzla – tieto úseky musia mať buď všetky rovnaké zafarbenie, alebo všetky tri rôzne. Ak je možné takto uzol vyfarbiť, hovoríme, že daný uzol je trojofarbiteľný. Príkladom je trojlístkový uzol.

Ukázať, že trojofarbiteľnosť je naozaj uzlový invariant, však nie je také jednoduché. Problémom je, že jeden a ten istý uzol možno zakresliť do roviny rozličnými spôsobmi. Nemôže sa teda napríklad stať, náčrtmi jedného uzla sa dá prejsť pomocou iba niekoľkých operácií, tzv. Reidemeisterových ťahov. Stačí teda ukázať, že vykonanie týchto operácií nepokazí trojofarbiteľnosť uzla. To už nie je také náročné. Výsledkom je skutočnosť, že trojofarbiteľnosť je naozaj invariant – ak teda máme dva uzly, z ktorých jeden je trojofarbiteľný a druhý nie je, vieme, že nevyhnutne ide o rozdielne uzly.
V súčasnosti poznáme mnoho uzlových invariantov, typicky omnoho sofistikovanejších ako trojofarbiteľnosť. Prekvapivá je však skutočnosť, že časť z nich sa dá získať pomocou fyzikálnych úvah pochádzajúcich z oblasti kvantovej mechaniky a kvantovej teórie poľa. Aj to robí z modernej teórie uzlov dôležitú (a pôvabnú) križovatku viacerých vedeckých disciplín.
Fridrich Valach
Imperial College London
Viac podobných článkov nájdete na stránke vedator.space.



