Praktické potreby už v období starého Egypta utvárali matematiku ako metódu riešenia hospodárskych problémov (spotreba osiva, výnos z polí, meračské práce, stavba pyramíd).
Charakteristika egyptského pisára
Jeden z moderných historických názorov ponúka túto charakteristiku: Pisári (hierogramati, harpedonapti) tvorili tretiu kastu egyptských kňazov. V náboženských sprievodoch sa objavoval pisár na treťom mieste. Mal na hlave perá, v rukách držal knihu, pravítko, kalamár a tyčinku na písanie. Do jeho povinností patrilo všetko, čo sa vzťahovalo na stavebnú činnosť chrámov a ich pozemkového vlastníctva. Pisári museli poznať hieroglyfy a vonkajšie ozdoby chrámov, vedieť zakresľovať tok Nílu. Mali vedomosti z astronómie, geometrie i geografie. Povinné znalosti pre nich sústredili do deviatich zo 42 kníh, ktoré boli určené pre nevyhnutné poznatky šiestich vrstiev kňazskej kasty. Je zrejmé, že matematické, astronomické a geografické vedomosti tvorili hlavnú odbornosť týchto pisárov.
Významné papyrusy
Jeden z najstarších písomných matematických dokumentov (z obdobia asi 18. – 16. stor. pred n. l.) je Rhindov papyrus (534 × 32 cm), papyrusový zvitok nájdený roku 1858. Odkúpil ho škótsky antikvariátnik H. Rhind, je však uložený v Britskom múzeu v Londýne. Prezýva sa aj Ahmesov papyrus. Je na ňom 84 úloh napísaných pisárom Ahmesom. Text začína takto: Presné počítanie – vstup do znalostí všetkých existujúcich vecí a všetkých temných záhad. Toto dielo písal Ahmes okolo roku 1650 pred n. l. ako opis spisu z obdobia rokov 2000 až 1800 pred n. l. a možno niektoré poznatky sú až z časov stavby pyramíd od Imhotepa okolo roku 2800 pred n. l. Z papyrusu sa môžeme dočítať o už vtedy významnom postavení matematiky, ktorá je zasvätená dokonalému a podrobnému skúmaniu všetkých vecí, pochopeniu ich podstaty a poznaniu všetkých tajomstiev.
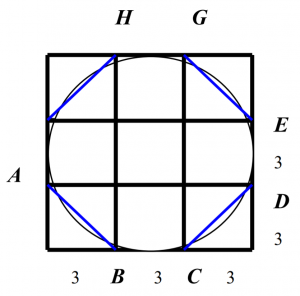V jednej úlohe sa predpokladá, že plocha kruhu s priemerom 9 jednotiek je rovnaká ako plocha štvorca so stranou dlhou 8 jednotiek. Možno to vysvetliť aj takto: Ak danej kružnici, napr. s priemerom d = 9, opíšeme štvorec a rozdelíme stranu štvorca na tri časti (pozri obrázok), dostaneme 9 menších štvorcov, môžeme vytvoriť v rohoch veľkého štvorca trojuholníky, aby sme dostali osemuholník ABCDEFGH. Veľkosť plochy tohto osemuholníka sa príliš nelíši od veľkosti plochy kruhu vpísaného do štvorca. Obsah osemuholníka je zhodný s plochou piatich menších štvorcov sčítaných s plochou štyroch trojuholníkov v rohoch (5×32 + 4×9/2 = 45 + 18 = 63). To je približne 64 = 82. Tak sa dá obsah kruhu s priemerom 9 jednotiek približne odhadnúť ako obsah štvorca so stranou 8 jednotiek. Potom (v našom zápise) je obsah kruhu π×(9/2)2 = 82 a teda π = (64×4)/81 = 4×(8/9)2 = (16/9)2 = 3,16049… Tak sa už nečudujeme, že Egypťania tohto obdobia mali π = (16/9)2.
Dušan Jedinák
