Občas sa stáva, že nevinne vyzerajúca úloha z bežného života vedie k prekvapivo zaujímavej a hlbokej matematike. Napríklad také delenie jabĺk medzi kamarátov môže človeka priviesť k prvočíslam a rozdeľovanie pôdy zasa k trigonometrii. K čomu nás môže priviesť stavanie veže z kociek?
Predstavme si, že máme k dispozícii obrovské množstvo kociek a chceme z nich postaviť vežu. Stavanie kociek priamo jednu na druhú je však nuda, a tak sa rozhodneme vežu postaviť nakrivo. Samozrejme, ak ju postavíme priveľmi nakrivo, tak spadne. A to nás vedie k zaujímavej otázke: Akú najkrivšiu vežu možno postaviť? Je napríklad možné postaviť vežu tak krivo, aby priemet vrchnej kocky nadol ležal úplne pomimo najspodnejšej kocky? Ak áno, ako najďalej od spodku veže môže ležať tento priemet? Inak povedané, ako ďaleko sa môže veža nakloniť?
Riešenie
Ako prvý krok si všimnime, že rovnaký výsledok dostaneme, ak budeme uvažovať sadu rovnakých kvádrov namiesto kociek – tie sa nám budú aj lepšie kresliť. Pre konkrétnosť si predstavme, že tieto kvádre-tehličky majú dĺžku 2. (Áno, dĺžka 1 by možno bola trochu prirodzenejšia, no autor tohto textu vie, že konečný výsledok bude trochu krajší, ak si vezmeme tehličky takejto dĺžky.)
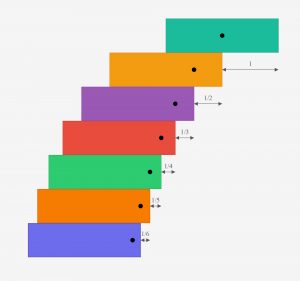
Ako druhý a zásadnejší krok si treba uvedomiť, že veža postavená z takýchto kvádrikov nespadne práve vtedy, keď pre každú jednu tehličku platí nasledovná podmienka: Ťažisko celej časti stavby, ktorá stojí nad uvedenou tehličkou, sa nachádza nad ňou a nie mimo nej. Vezmime si príklad dvoch tehličiek. Ťažisko tej hornej je v jej strede – a veža z dvoch tehličiek sa nezrúti práve vtedy, keď bude stred vrchnej tehličky ležať nad spodnou a nebude cez ňu prečnievať. V tomto prípade teda najväčší previs bude mať dĺžku 1. Na obrázku tomu zodpovedá vrchný tandem tyrkysovej a oranžovej tehličky.
Teraz si predstavme, že máme tri tehličky. Skúsme využiť našu skonštruovanú dvojtehličkovú vežu a posadiť ju celú na tretiu fialovú tehličku. Po spočítaní polohy ťažiska zistíme, že maximálny možný previs tyrkysovej tehličky nad fialovou bude tentoraz ½. A tak ďalej – zakaždým vyrátame polohu ťažiska a na spodok pridáme ďalší kváder tak, aby ťažisko konštrukcie nad ním neležalo mimo neho. Po krátkom výpočte zisťujeme, že ďalšie tehličky postupne môžeme posunúť o 1/3, 1/4, 1/5 atď. Pre celkový previs teda dostaneme nekonečný súčet S = 1 + 1/2 + 1/3 + 1/4 + 1/5 +…
Druhá časť
Aká je presná hodnota celkového súčtu S? Nekonečné rady tohto typu sú často celkom zaujímavé, napríklad súčet radu ½ + ¼ + ⅛ +… dáva dokopy presne 1 a zodpovedá situácii, keď si rozkrojíme koláč na dve polovice, jednu z polovíc opäť rozkrojíme napoly, jednu zo získaných polovíc opäť rozkrojíme napoly atď., pričom dostaneme nekonečne veľa kúskov, ktoré však dokopy dajú práve jeden celý koláč.
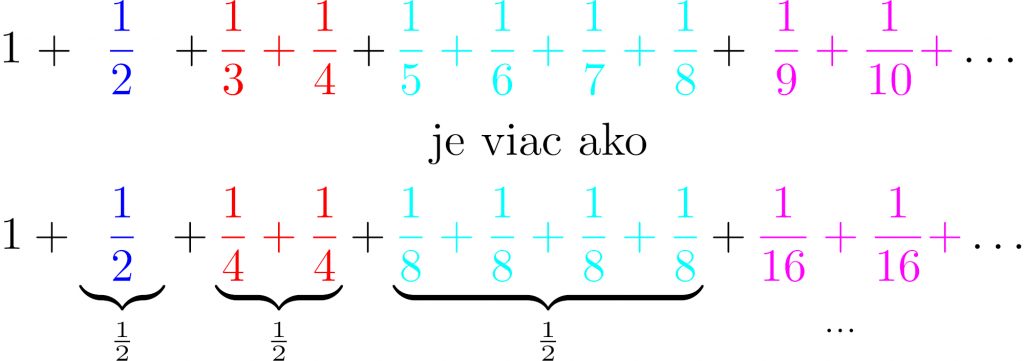
V našom prípade je však výsledok ešte zaujímavejší. Ako si v 14. storočí všimol francúzsky filozof Mikuláš z Oresme, nech už je číslo S akékoľvek, bude určite väčšie ako súčet istej inej skupiny čísel (pozri spodný obrázok). Pritom využívame skutočnosť, že napríklad 1/3 > 1/4, 1/5 > 1/8 atď. Lenže táto druhá postupnosť zodpovedá súčtu 1 + 1/2 + 1/2 + 1/2 + 1/2 +…, ktorý však rastie nad všetky medze, a teda je nekonečný. A preto je aj S nekonečné. V matematike vravíme, že uvedený rad diverguje. Inak povedané, pri dostatočne veľkom počte kociek možno postaviť vežu, ktorá sa vychýli viac než ľubovoľná vopred stanovená vzdialenosť.
Fridrich Valach
University of Hertfordshire
Spojené kráľovstvo
Viac podobných článkov nájdete na stránke vedator.space. Vedátora môžete sledovať aj prostredníctvom bezplatnej mobilnej aplikácie.