Ako vieme, objem kvádra vypočítame podľa jednoduchého vzorca V = a · b · c, teda súčinom dĺžok jeho troch strán. Keď sa však pozrieme na tvar pre výpočet objemu gule V = 4/3 · π · r3, zistíme, že jeho odvodenie je už náročnejšie. Ako tento výpočet vznikol?
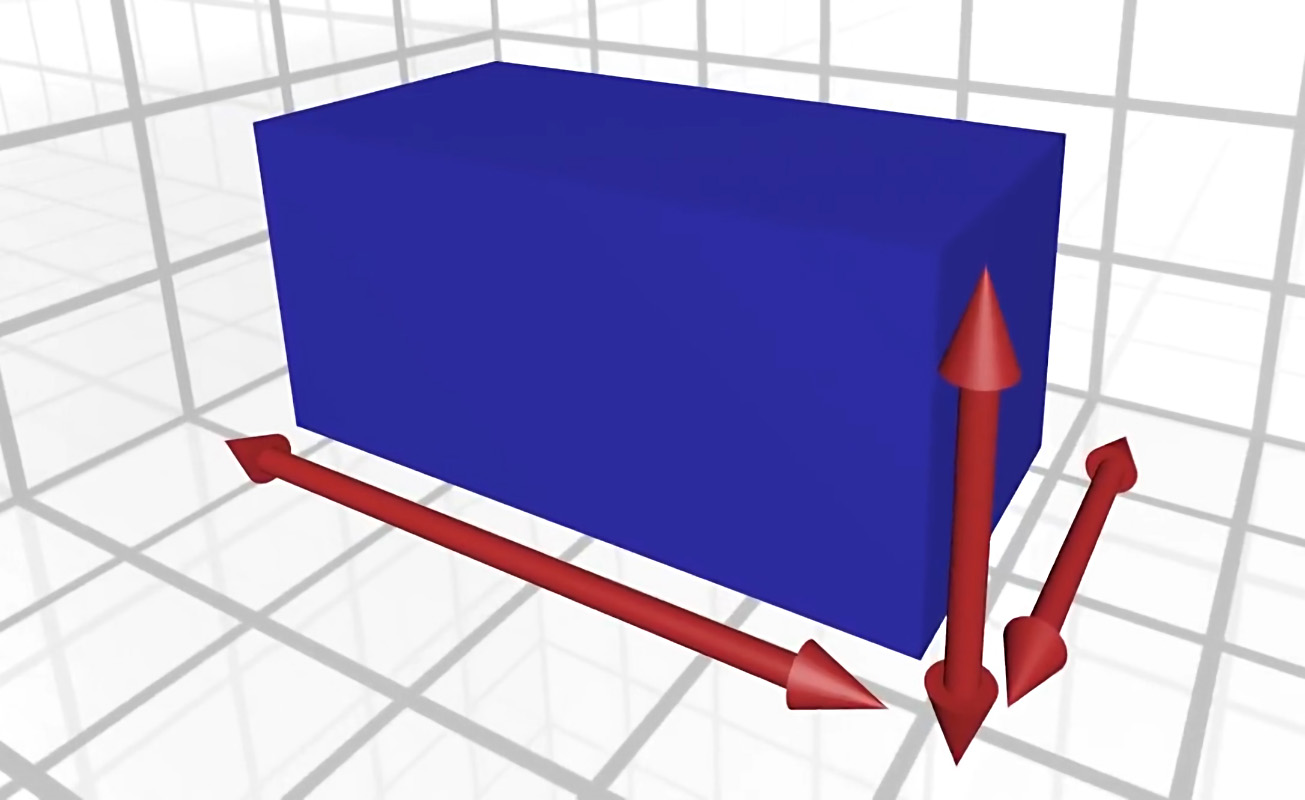
Uvažujme najprv o kvádri a vzorci na výpočet jeho objemu. Kváder má dané rozmery, daný počet dielikov v každom smere. Na lepšiu predstavu si vytváranie trojrozmerného telesa vizualizujme ako rozťahovanie hmoty najprv z bodu až do danej dĺžky kvádra. Vznikne nám tak úsečka, ktorú potom tiež roztiahneme v druhom smere až do danej šírky kvádra. Následne dostaneme plochu, ktorú do tretice roztiahneme smerom nahor do potrebnej výšky kvádra.
Na rozdiel od kvádra tvoria vzorec gule V = 4/3 · π · r3 na prvý pohľad tri nesúvisiace veci: r3 vyjadruje objem kocky s dĺžkou strán r, číslo π je známa matematická konštanta s hodnotou 3,14 pre prácu s kružnicami a k tomu zlomok 4/3.
Na rozlúštenie vzorca môžeme využiť integrálny počet.
Čo je integrál?
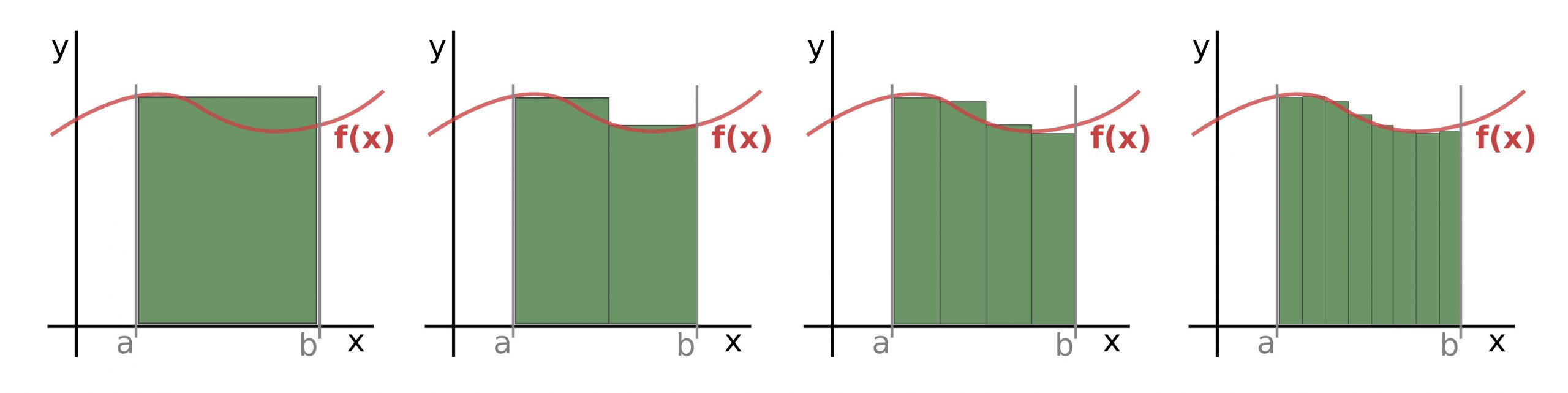
Integrály a derivácie sú základné stavebné kamene časti matematiky nazývanej matematická analýza. Určitý integrál nezápornej funkcie medzi dvomi bodmi a, b na osi x sa rovná ploche pod krivkou tejto funkcie, zdola ohraničenou práve osou x. Výpočet integrálu je odvodený od postupného zmenšovania obdĺžnikov pod danou funkciou.
Keď chceme vyrátať plochu pod funkciou, najprv ju aproximujeme (nahradíme) jedným obdĺžnikom, resp. jeho obsahom, čím dostaneme veľmi nepresné číslo. Keď však postupne obdĺžniky zmenšujeme na šírku, pričom horné hrany obdĺžnikov kopírujú tvar danej funkcie, dostávame presnejšiu hodnotu. Pokiaľ ich zmenšujeme donekonečna, získame absolútne presnú hodnotu plochy.
Integrály nám teda okrem iného pomáhajú aj s dĺžkami kriviek, obsahmi plôch v dvoch rozmeroch a objemami trojrozmerných telies.
Pri kvádri…
Zoberme si teraz konkrétny kváder, napríklad 8 × 4 × 3 umiestnený v priestorových súradniciach. Štandardne vypočítať jeho objem je ľahké, výsledok je 96. Skomplikujme si život a skúsme to pomocou integrálov. Nebudeme integrovať nič zložité, iba číslo 1, no budeme počítať až trojný integrál. Trojný integrál zavedieme tak, že integrujeme tri do seba vložené integrály, postupne jeden po druhom. Hranice integrovania každého z troch integrálov budú hranicami daného kvádra v karteziánskej pravouhlej sústave súradníc.
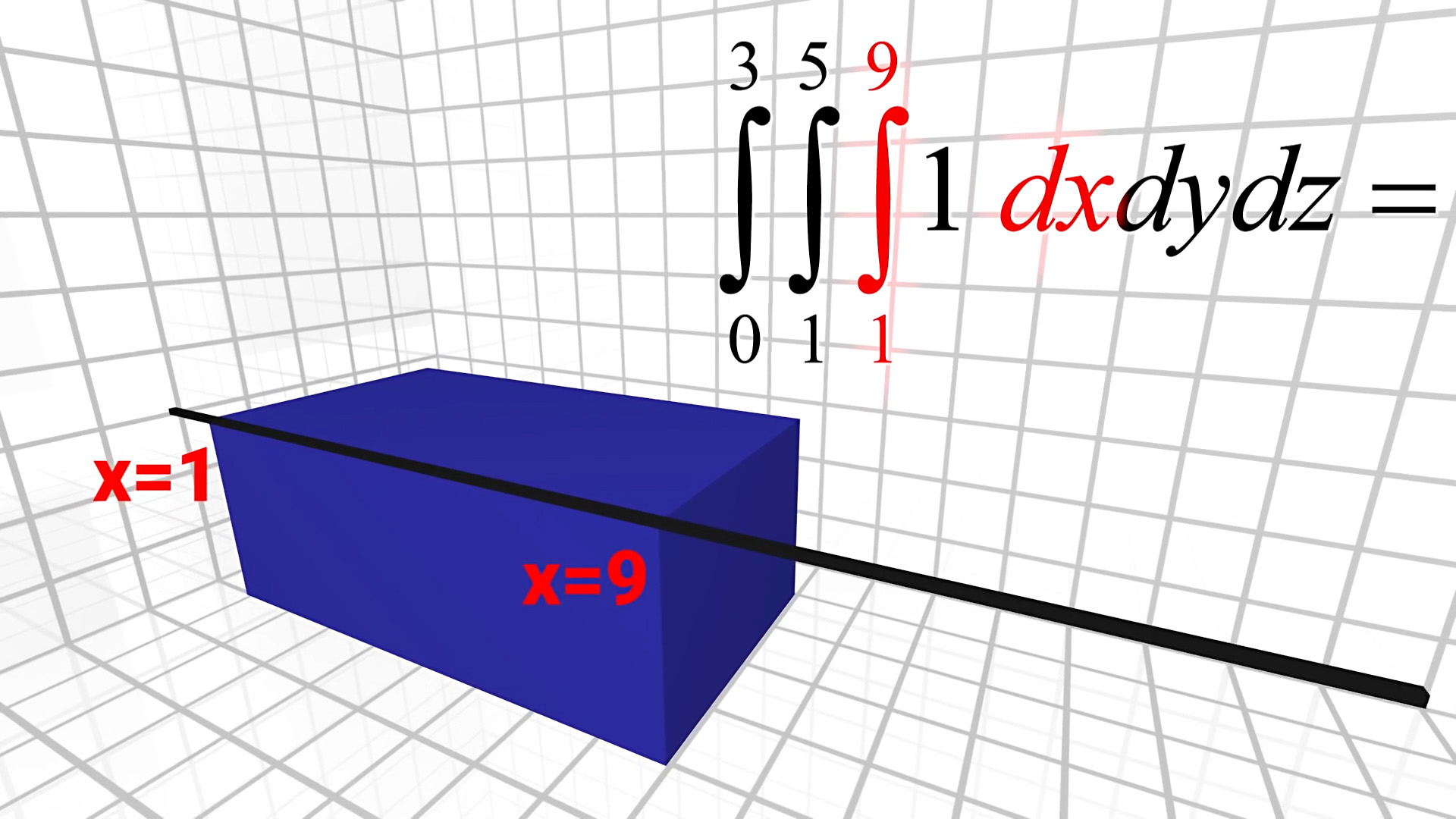
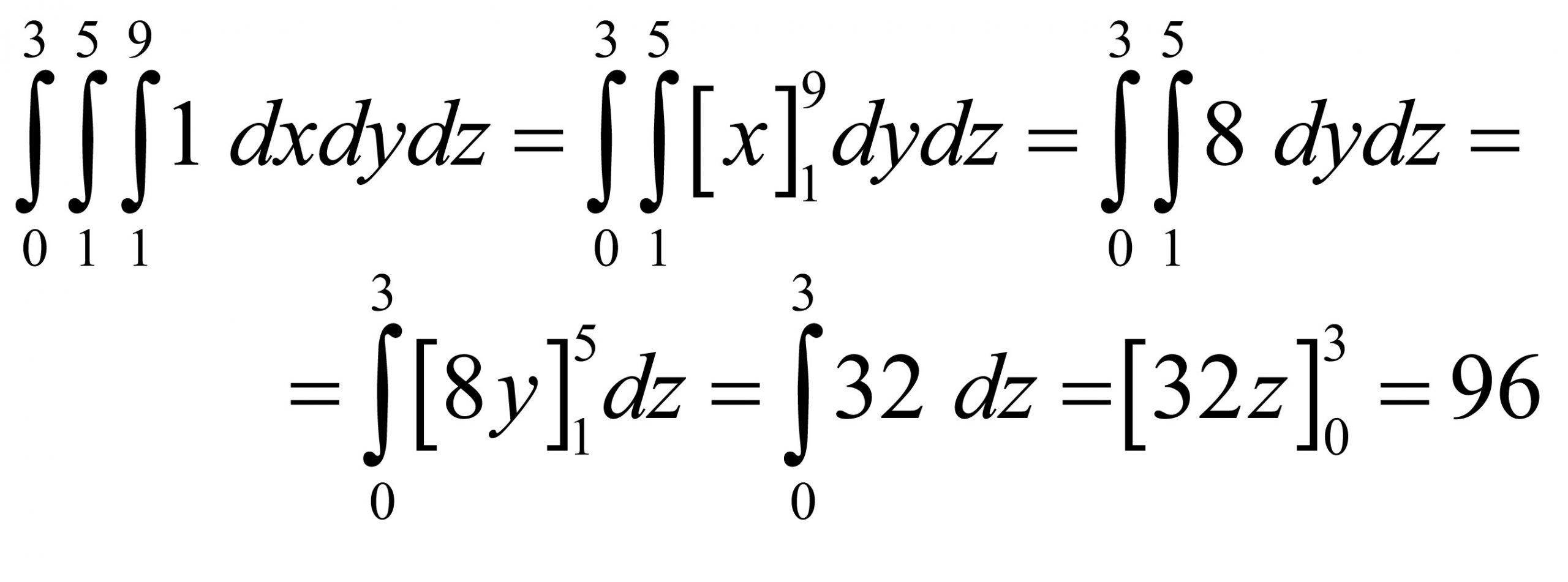
Spomeňme si na naťahovanie hmoty v úvode článku. Prvý integrál znázorňuje dĺžku krivky v smere x. Druhým integrálom pridáme výpočet plochy s dĺžkou a šírkou kvádra. A následne tretí integrál doplní objem do výšky. Po vypočítaní tohto trojného integrálu dostávame hodnotu 96 – rovnakú hodnotu, ako pri počítaní objemu kvádra klasickým spôsobom.

… a pri guli
Podobný postup použijeme aj pre guľu. Pri kvádri sme používali na jeho zadefinovanie v priestore klasické pravouhlé súradnice, teda šírku, dĺžku, výšku. To by bol pri pracovaní s guľou problém, keďže chceme použiť rovnaký princíp rozťahovania hmoty ako pri kvádri. Pre túto predstavu rozťahovania hmoty platí pravidlo, že môžeme používať iba tie smery, v akých súradniciach aktuálne pracujeme. Keby sme z bodu mali hmotu rozťahovať iba tými tromi smermi ako pri kvádri, nedokázali by sme ju roztiahnuť do tvaru gule.
Preto si zavedieme tzv. sférické súradnice, kde je pozícia bodu v priestore určená polomerom (resp. vzdialenosťou od stredu súradnicovej sústavy) a dvomi uhlami (o koľko stupňov je bod vychýlený od roviny x a o koľko od roviny y).
Pre prevod súradníc bodu z karteziánskych pravouhlých súradníc do sférických súradníc existuje jednoduchý vzorec. Preto budeme pri počítaní objemu gule pomocou integrálov počítať nie s číslom 1, ale so zložitejším výrazom.
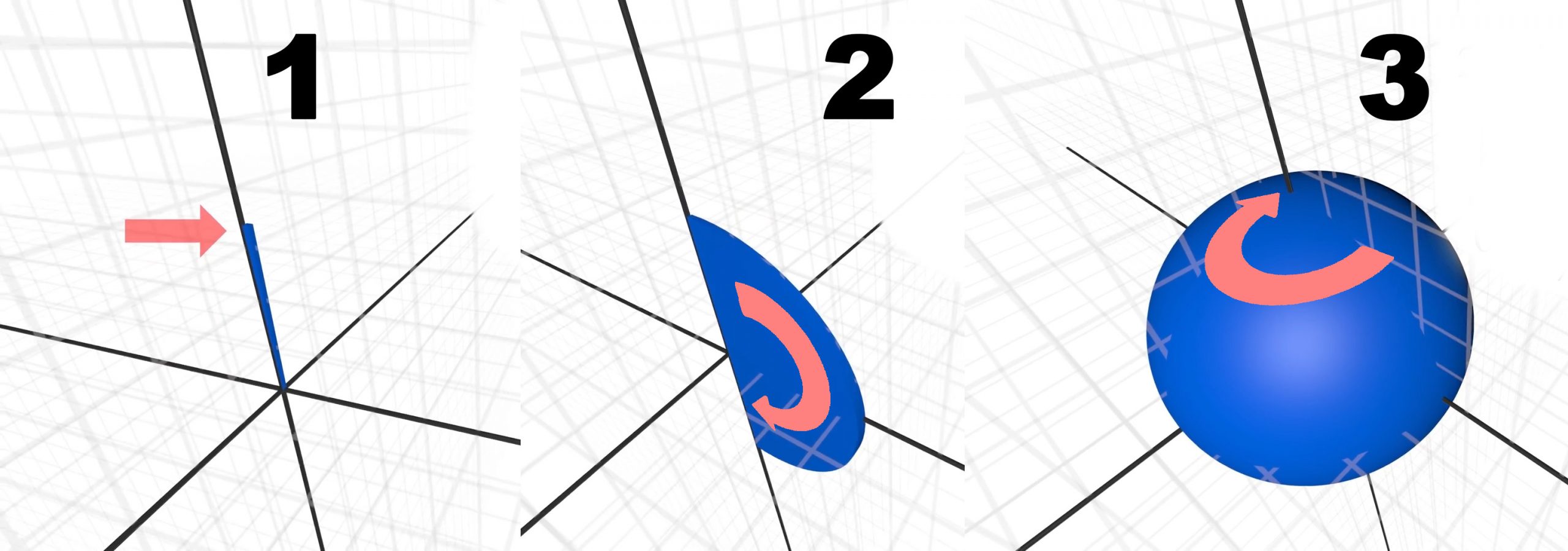
Ťahanie hmoty
Tentoraz pri rozťahovaní hmoty z jedného bodu vytiahneme hmotu do dĺžky polomeru gule, ktorý sa zvyčajne označuje písmenom r. Vznikne úsečka, ktorú otočíme okolo osi o 180 stupňov, pričom dostaneme polkruh. Ten napokon opäť otočíme o 360 stupňov okolo druhej osi a roztiahnutím hmoty vznikla guľa.
V ďalšom kroku budeme počítať trojný integrál v troch hraniciach podľa sférických súradníc. Tu však musíme dať pozor aj na poradie integrovania. Zatiaľ čo pri kvádri nezáležalo na tom, či sme hmotu rozťahovali najprv do šírky a potom do dĺžky (alebo v opačnom poradí) a vždy sme dostali ten istý kváder, pri guli je poradie dôležité. Napríklad, keby sme po roztiahnutí hmoty do polomeru danú úsečku následne otáčali podľa tej osi, podľa ktorej máme úsečku otáčať až v treťom kroku, tak by nám po jej otočení nevznikol polkruh, ale ostala by úsečka. Rovnako, keby sme ako prvý v poradí otáčali bod, tak by sa iba otáčal na mieste a nevznikla by žiadna hmota.
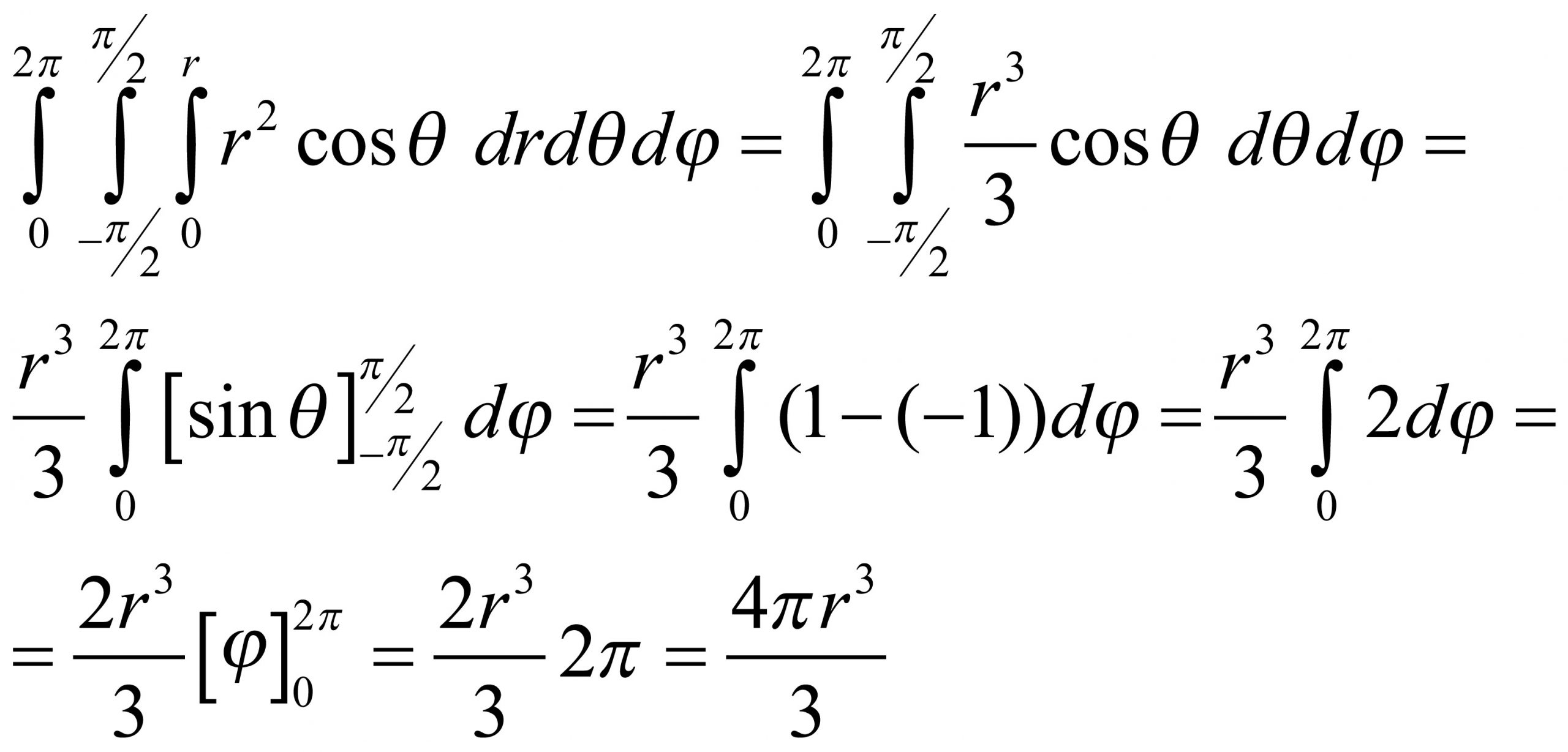
Všeobecný vzorec
Ako bude vyzerať konkrétny výpočet? Najskôr budeme integrovať pre dĺžku krivky od stredu súradnicovej sústavy 0 po dĺžku polomeru gule r. Potom integrujeme otočenie okolo 180 stupňov do polkruhu, od -π/2 po π/2, a nakoniec otočenie do tvaru gule o 360 stupňov, od 0 po 2π. Pre už spomínaný vzorec pre transformáciu súradníc však nebudeme integrovať číslo 1, ale tzv. jakobián, ktorý má tvar r2 · cosθ. Presné odôvodnenie tohto tvaru odporúčame skôr na samoštúdium pre zanietených matematikov.
Integrál sme počítali so všeobecnými hodnotami a nedosadzovali sme čísla konkrétnej gule. Preto nám aj vyšiel všeobecný tvar na výpočet objemu gule, a nie konečné číslo pre jej objem.
Rovnakým princípom sa dajú odvodiť všeobecné vzorce napríklad pre objem valca, obsah kruhu a mnohé iné štandardné útvary. Podľa potreby inžinierov je možné odvodiť aj naozaj komplikované všeobecné vzorce pre objemy komplexných útvarov, ktoré sú v danej oblasti potrebné, či už pri architektonických stavbách, inžinierskych prácach, výpočtoch v astronómii a podobne. Matematika je všadeprítomná, aj keď niekedy veľmi skryto.
Text a vizualizácie Stanislav Griguš
Fakulta matematiky, fyziky a informatiky UK v Bratislave



