Skúste bez väčšieho rozmýšľania povedať, či opakovaním veľkého množstva náhodných procesov dostanete niečo, čo bude náhodné viac alebo menej. Ak máte, môžeme sa pozrieť na to, ako to je.

Väčšina z nás má intuitívnu predstavu o tom, čo je náhodná veličina. Je to niečo, čoho výsledok nemáme pod kontrolou. Zároveň si predstavíme hádzanie kockou alebo hod šípky do terča so zavretými očami (alebo aj s otvorenými). Predchádzajúca úloha je teda o opakovaní niečoho podobného veľmi veľakrát.
Priemerná hodnota
Zoberme si hádzanie kockou. Hodíme kocku, zapíšeme si číslo a znova kocku hodíme. To si tiež zapíšeme a takto to opakujeme. Po každom hode spočítame priemer dovtedajších hodnôt. Napriek tomu, že samotné hody sú úplne náhodné, priemer sa po začiatočných osciláciách veľmi rýchlo ustáli na čísle 3,5.
Nie je ťažké prísť na vysvetlenie tohto javu. Hodnoty na kocke sú náhodné a menia sa medzi 1 a 6. No odchýlky nad priemerom 3,5 budú v súčtoch vykompenzované odchýlkami pod priemerom a celkom rýchlo sa navzájom vyrušia. Ako priemer dostaneme hodnotu 3,5 bez ohľadu na to, aké čísla sme na kocke hodili. Podobným spôsobom takmer vždy meriame priemer akéhokoľvek náhodného rozdelenia.
Zmenšovanie disperzie
Môžeme vyskúšať ešte inú vec – nehádzať kockou veľakrát, ale iba nejaký konečný počet a spraviť iba obyčajný súčet. Napríklad pri desiatich hodoch by sme ako súčet očakávali 35. No keďže hádzanie je náhodné, aj výsledný súčet bude náhodný. Podstatné je, že pri viacerých opakovaniach týchto desiatich hodov bude výsledok oscilovať menej ako v prípade hádzania jednou kockou.
Tejto charakteristike sa hovorí disperzia a všeobecne popisuje, ako široko okolo priemernej hodnoty je náhodná veličina rozdelená. A pri opakovaní sa disperzia zmenšuje! (Táto veta si ako jediná v celom texte zaslúžila výkričník.) V prvom príklade ako absolútne číslo, v druhom v porovnaní s priemernou hodnotou.
Dostávame teda možno trochu kontraintuitívnu odpoveď, že veľa náhodných udalostí spolu vytvorí niečo menej náhodné – a pri istých otázkach dokonca úplne predvídateľné.
Normálne rozdelenie
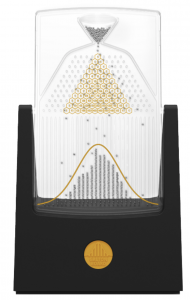
V matematike sa tomuto výsledku hovorí centrálna limitná veta. Dokonca sa dá ukázať, že so zvyšovaním počtu opakovaní sa rozdelenie priemeru približuje ku Gaussovmu rozdeleniu – je teda univerzálne bez ohľadu na pôvodné náhodné rozdelenie. A tiež to, že šírka tohto rozdelenia sa postupne zmenšuje. Výsledkom potom je, že na Gaussovo rozdelenie narazíme na každom kroku. Výška ľudí, nepresnosti volebných prieskumov, chyby meraní – to všetko sa dá popísať Gaussovým rozdelením. Zašlo to tak ďaleko, že zväčša sa v praxi rozdelenie už ani explicitne nespomína a hovoríme len o stredných hodnotách a disperzii.
Predpoklady centrálnej limitnej vety sú celkovo mierne a v podstate stačí, aby malo pôvodné rozdelenie náhodných veličín konečnú disperziu. Potrebujeme, aby veľmi nepriemerné hodnoty boli veľmi nepravdepodobné. To je zväčša splnené, ale sú situácie, keď to neplatí a treba si dávať pozor – príkladom sú niektoré udalosti na akciových burzách, ktoré môžu viesť k ich krachom.
Náhodnosť počasia
Na záver môžeme ešte odpovedať na prirodzenú otázku o počasí. To sa zdá byť celkom náhodné, aj keď podľa toho, čo sme doteraz písali, by také byť nemalo. Háčik je v tom, že náhodnosť počasia, na ktorú sme zvyknutí a hromžíme, keď prší, aj keď nemalo, má korene niekde inde – v samotných rovniciach pre atmosférické podmienky – a nie v náhodnosti pohybu jednotlivých molekúl. Dôsledkom toho, čo sme písali, a veľmi veľkého počtu molekúl v atmosfére je to, že aj keď je správanie sa jednotlivých častíc úplne náhodné, nakoniec sa predsa len nejaké rovnice dajú napísať a viac či menej úspešne riešiť.
Juraj Tekel
Fakulta matematiky, fyziky a informatiky
Univerzita Komenského v Bratislave
Viac podobných článkov nájdete na stránke vedator.space.



