Existuje niečo, čo nedokážu ani počítače budúcnosti? O hlavolamoch, počítačoch a fyzike a o tom, čo nám príroda dovolí a nedovolí vypočítať, sme sa rozprávali s Danielom Nagajom z Fyzikálneho ústavu SAV.

Čo sú hlavolamy? Prečo ľudí baví riešiť ich?
Všetci poznáme hlavolamy – malé úlohy na rozmýšľanie s jasným cieľom. Drevené skladacie, drôtené rozpájacie, papierové tangramy alebo dopĺňacie sudoku. Pre mňa je to skvelé mozgové cvičenie, ktoré v sebe skrýva peknú matematiku. Pri dobrom hlavolame musím vystúpiť z bežného spôsobu rozmýšľania a byť schopný nájsť nejakú efektívnu skratku. Mám rád, keď mi veci do seba konečne zapadnú a prídem problému na koreň, namiesto toho, aby som to len náhodne skúšal a vyriešil so šťastím. Myslím si, že existuje typ ľudí, pre ktorých sú až neodolateľným pokušením. Zadaním dobrej úlohy viem napríklad pár svojich kamarátov odpísať, pretože nemôžu robiť nič ďalšie, kým ju nevyriešia.

Daniel Nagaj je kvantový fyzik, ktorý rád cestoval, chodil po horách a dirigoval detský zbor. Teraz však všetok voľný čas trávi s vlastnými deťmi. Vyštudoval Fakultu matematiky, fyziky a informatiky Univerzity Komenského v Bratislave a doktorát si robil na Massachusettskej technickej univerzite v USA. Po rokoch v zahraničí sa vrátil a dlhodobo sa venuje výskumu na Fyzikálnom ústave Slovenskej akadémie vied v Bratislave. Rozmýšľa nad tým, čo nám príroda dovolí vypočítať – ale aj nad tým, čo sa nebude dať efektívne vypočítať ani na počítačoch, ktoré ešte nemáme.
Prečo sú niektoré úlohy ťažšie ako iné?
Základná otázka je, či pre daný hlavolam existuje krátka jasná cesta k riešeniu. Napríklad stratégia držať sa pravej steny pri prechode bludiskom. Niekedy sa zase zdá, že nevieme robiť takmer nič iné, iba skúšať všetky možnosti. Takto frustrujúcim je pre mňa pentomino. Ako zistiť, či som na dobrej ceste? Niečo, čo dlho vyzerá sľubne, ešte vôbec neznamená, že to povedie k riešeniu.
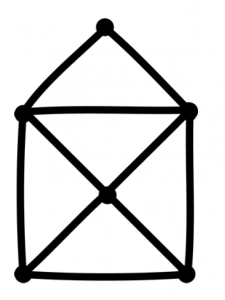
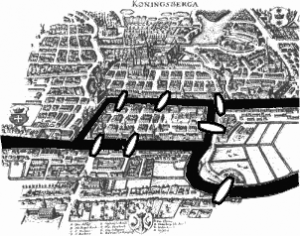
Na druhej strane existujú aj ľahké hlavolamy, kde človek rýchlo vidí, alebo si matematicky odôvodní, ktoré možnosti môže vylúčiť. Napríklad pri kreslení domčeka jedným ťahom (obr. 1) prídeme na to, že sa dá začať len v dvoch bodoch. Táto úloha je stará – vedeli by ste napríklad ľudom z Königsbergu dokázať, že prejsť sa po všetkých mostoch a po každom pritom prejsť iba raz sa naozaj nedá (obr. 2).
Veľmi podobná úloha je táto: poskáčte šachovnicu (obr. 3) šachovým jazdcom tak, aby ste na každé políčko skočili len raz a vrátili sa na štart. Je to príklad hľadania hamiltonovského cyklu v grafe a o úlohe vieme, že patrí medzi najťažšie hlavolamy triedy NP. V teórii zložitosti triedu úloh, ktorých riešenia vieme ľahko skontrolovať, voláme NP, a triedu úloh, ktorých riešenia vieme ľahko nájsť, nazývame P.
Nevieme naozaj, prečo sú tie najťažšie (NP-úplné) úlohy v triede NP také ťažké. Vieme isto, že doteraz odolali všetkým našim pokusom o efektívne hľadanie riešení. No je nečakane ťažké dokázať, že sa to naozaj nikdy nikomu nepodarí.
Ktoré druhy hlavolamov je lepšie prenechať počítaču?
Práve pre zložité optimalizačné úlohy, pre ktoré nemáme efektívne riešenia, vieme využiť počítače. Mnoho možností môžu za nás vyskúšať oveľa rýchlejšie, ako by sme to dokázali sami. Vďaka tomu vieme v súčasnosti hľadať optimálne rozvrhy pre školy, vymýšľať, ako múdro naskladať a poprepájať na čipe mnoho tranzistorov alebo optimalizovať distribučné siete elektrární.
Čo je algoritmus?
Algoritmus je v podstate popis jasných krokov pri hľadaní riešenia. Napríklad viazanie šnúrok, násobenie dvoch dlhých čísel alebo náhodné kráčanie (v každom kroku si hoďte mincou, spravte krok a pozrite sa, či ste nenašli cieľ).

Aké sú obmedzenia klasických počítačov pri riešení hlavolamov?
Podstatné je, koľko krokov náš algoritmus bude potrebovať v najhoršom prípade pri riešení úlohy danej veľkosti. Násobiť čísla je ľahké (skúste si to napríklad pre 673 × 3 = ?), náročnosť základného algoritmu rastie kvadraticky s počtom cifier a násobiť 300-ciferné čísla je pre počítač hračka. Na druhej strane rozkladať čísla na prvočíselné delitele je ťažké (skúste si to pre 2 021 = ? × ?). Najlepší algoritmus, ktorý pre túto úlohu v súčasnosti máme, o rozkladaní 300-ciferných čísel nemôže ani snívať. Na tom je založená bezpečnosť šifrovania štandardnou metódou RSA. A tu do hry prichádza môj odbor, kvantové počítače, v ktorom Peter Shor v roku 1993 objavil efektívny kvantový algoritmus. Už len poskladať niekoľkotisícqubitový kvantový počítač s nízkou chybovosťou operácií a mohli by sme terajšie šifry čítať. To je, samozrejme, zatiaľ len sen.
Oveľa ťažšou úlohou sú však napríklad simulácie priestorového usporiadania atómov v chemických molekulách (proteínoch). No aj tam ideme neuveriteľne dopredu a som si istý, že v dohľadnom čase zase pohneme hranice toho, čo dokážeme vypočítať a nasimulovať.
Za rozhovor ďakuje redakcia Quarku



