V tretej časti série článkov na tému vysvetliteľnej a transparentnej umelej inteligencie sa pozrieme na dve kategórie jej modelov – transparentné modely a modely typu čierna skrinka.
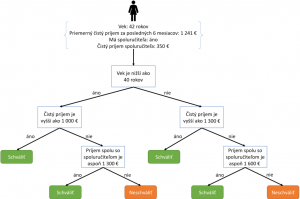
Aké sú medzi nimi rozdiely a prečo používame aj netransparentné modely, keď je schopnosť pochopiť ich predpovede taká dôležitá? Ktoré modely môžeme považovať za transparentné a ktoré si, naopak, vyžadujú dodatočnú interpretáciu a vysvetlenie ich predpovedí?
Transparentné modely a čierne skrinky
Transparentné modely umelej inteligencie sú také, pri ktorých vieme pochopiť nielen to, ako fungujú po algoritmickej stránke, ale aj to, prečo sa rozhodujú tak, ako sa rozhodujú. Dokážeme teda porozumieť, ako modely premýšľajú a aké poznatky získali o reálnom svete. Tieto modely sú typicky staršie, menej výkonné a jednoduchšie.
Príkladom transparentného modelu sú rozhodovacie stromy s malým počtom uzlov. V rozhodovacích stromoch sú poznatky, na základe ktorých model vytvorí predpoveď pre vstup, vyjadrené explicitne ako pravidlá, napr. AK má človek príjem viac ako 1 000 eur A má menej ako 40 rokov, TAK je možné schváliť mu úver vo výške 30 000 eur.
Aj pre komplexné modely typu čierna skrinka platí, že vieme pochopiť, ako pracujú. Rozumieme ich mechanike a matematickým operáciám, ktoré sa využívajú v procese učenia a rozhodovania. Tieto modely sú však také komplexné, že nie je možné úplne simulovať to, ako prišli k rozhodnutiu. Presnejšie povedané, nerozumieme tomu, aké podnety a poznatky zakódované v modeli k nemu viedli. Jednotlivé operácie, ktoré prebiehajú v modeli, pritom môžu byť veľmi jednoduché, napríklad sčítanie a násobenie. Keď však model obsahuje takýchto operácií milióny až miliardy, nie je v ľudských silách simulovať alebo aspoň skontrolovať efekt každej z nich.
Neurónové siete
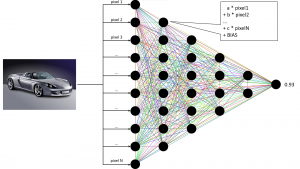
Typickým predstaviteľom modelov typu čierna skrinka sú hlboké neurónové siete. Kým v rozhodovacích stromoch sú poznatky vyjadrené explicitne ako pravidlá, v prípade neurónových sietí sú zapísané vo forme zväčša maličkých číselných hodnôt – parametrov modelu. Predpoveď je potom vytvorená vďaka postupnosti matematických operácií (najčastejšie nad maticami a vektormi), ktoré transformujú vstupné dáta na finálnu predpoveď modelu.
Ilustráciu toho, ako neuróny v skrytých vrstvách kombinujú a postupne filtrujú vstupy pomocou parametrov, ponúka obrázok z prvej časti série. Do neho sme doplnili príklad výpočtu výstupu neurónu na prvej skrytej vrstve. Je zjavné, že na výpočet hodnoty jedného neurónu stačí vedieť sčítavať a násobiť.

Skrytá reprezentácia
Ďalším príkladom je klasifikácia čiernobielych obrázkov do piatich rôznych tried – auto, nákladiak, lietadlo, loď a kôň. Obrázok môžeme v počítači reprezentovať ako dvojdimenzionálnu mriežku čísel – maticu, v ktorej každá bunka obsahuje malé číslo. Toto číslo reprezentuje hodnotu konkrétneho pixelu (pri čiernobielom obrázku je biela farba reprezentovaná najčastejšie číslom 255, zatiaľ čo čierny pixel má hodnotu 0).
Neurónová sieť v prvej vrstve pomocou rôznych jednoduchých matematických operácií skombinuje tieto čísla so svojimi vlastnými parametrami. Vďaka tomu sa tento obrázok zmení na inú mriežku čísel. Tieto čísla už však nie sú hodnotami pixelov samotného obrázku, ale sú akýmsi filtrátom (odborne hovoríme o skrytej reprezentácii). Pri práci s obrazovými dátami sa na to v neurónových sieťach často využíva operácia konvolúcia, ktorá je základom mnohých filtrov v obrázkových editoroch (napr. Photoshop).
Druhá skrytá vrstva následne urobí presne to isté, čo prvá, no na jej vstupe už nie sú pixely obrázka, ale mriežka, ktorá vznikla v prvom kroku. Tento proces sa opakuje, až kým v neurónovej sieti nedôjdeme k poslednej, výstupnej vrstve, ktorej výstupom sú čísla. Každé z týchto čísel nám povie, do akej miery je model presvedčený, či je na obrázku auto, nákladiak, lietadlo, loď alebo kôň. Ak je najväčšie prvé číslo z tejto pätice, model je presvedčený, že na obrázku sa nachádza auto, ak druhé, bude to nákladiak atď.
Ako vidíme, v porovnaní s rozhodovacími stromami je pri neurónových sieťach veľmi náročné povedať, prečo bola predpoveď modelu taká, aká bola. Často iba nepriamo pozorujeme, ako sa vstup (napr. obrázok) vnútri modelu transformuje z jednej skrytej reprezentácie na inú a na základe toho môžeme odhadovať, čo sa v ňom deje.
Je transparentnosť vytlačená?

Väčšinu modelov, o ktorých možno vyhlásiť, že sú transparentné, tvoria jednoduchšie modely (rozhodovací proces v komplexných modeloch alebo modeloch s priveľa pravidlami človek nedokáže kognitívne obsiahnuť) s menšou modelovacou kapacitou. Mohlo by sa teda zdať, že ich využitie je malé a na zložitejšie úlohy nestačia.
Pravdou však je, že transparentné modely sa naďalej v praxi používajú. A to z toho dôvodu, že sú oblasti, v ktorých je transparentnosť minimálne taká dôležitá ako samotná výkonnosť modelu. V prestížnom časopise Nature nedávno vyšiel článok Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead, ktorý kritizuje bezdôvodné používanie príliš komplexných modelov, hoci by na riešenie daného problému úplne postačovali jednoduchšie, no transparentné modely.
Posudzovanie rizika recidívy
COMPAS je program, ktorý používajú viaceré súdy v USA na odhadnutie pravdepodobnosti, že človek, ktorý spáchal trestný čin, bude znovu konať protizákonne. Ide o program, ktorý priamo ovplyvňuje životy ľudí, no zároveň je netransparentný. Spoločnosť, ktorá program vyvíja, dokonca ani nezverejnila jeho princíp fungovania.
V uvedenom článku autorka programu Cynthia Rudinová uviedla alternatívnu metódu CORELS, ktorá je transparentná a pritom rovnako presná ako COMPAS.
Je prirodzené, že človek, o ktorom sa rozhoduje, či pôjde do väzenia alebo nie, chce poznať dôvod, pre ktorý sa tak súd rozhodol. Aj človek, ktorý spáchal nejaký priestupok, má totiž právo presvedčiť sa, že proces a dôvody, pre ktoré poputuje do väzenia, sú spravodlivé.
Aby to nebolo príliš jednoduché, vieme sa na tento problém pozrieť aj z iného pohľadu. Bolo by naozaj dobré, keby potenciálni zločinci presne vedeli, za akých okolností ich softvér označí ako vysokorizikových a za akých nie? Nemohlo by to viesť k snahe oklamať systém za účelom dosiahnutia nižšieho trestu?
Napriek nedostatkom, ktoré vyplývajú z komplexnosti, stále platí, že najvýkonnejšie modely sú zároveň najkomplexnejšie a ťažko vysvetliteľné a interpretovateľné.
Martin Tamajka
Kempelenov inštitút inteligentných technológií
Tento článok je súčasťou série Vysvetliteľná umelá inteligencia: od čiernych skriniek k transparentným modelom.
Projekt podporila Nadácia Pontis.
Anglickú verziu článku si môžete prečítať tu.



